Определение наибольшего общего делителя.

Наибольший общий делитель (НОД) – определение, примеры и свойства.

В этой статье мы изучим наибольший общий делитель (НОД). Сначала мы введем понятие общего делителя нескольких целых чисел и приведем примеры. Это позволит нам дать определение наибольшего общего делителя двух, а также трех и большего количества, дальше мы введем принятые обозначения, приведем примеры наибольших общих делителей. Наконец, перечислим основные свойства наибольшего общего делителя и представим их доказательства.

Навигация по странице.

Общие делители – определение, примеры

Чтобы подобраться к определению наибольшего общего делителя (кратко НОД), сначала узнаем, что такое общий делитель данных целых чисел.

В статье делители и кратные мы говорили о делителях одного данного целого числа. Сейчас мы будем одновременно рассматривать делители двух, трех и большего количества целых чисел, особо нас будут интересовать одинаковые, то есть, общие делители нескольких чисел.

Дадим определение общего делителя нескольких целых чисел.

Общий делитель нескольких целых чисел – это такое целое число, которое является делителем каждого из данных чисел.

Приведем несколько примеров общих делителей. Целое число 3 – это общий делитель двух целых чисел 9 и −12 , так как 3 является делителем и числа 9 (так как 9=3·3 ), и числа −12 (так как −12=3·(−4) ). Другими общими делителями чисел 3 и −12 являются числа 1 , −1 и −3 . Рассмотрим еще один пример. Четыре целых числа 3 , −11 , −8 и 19 имеют общие делители 1 и −1 .

Свойства делимости позволяют утверждать, что числа 1 и −1 являются делителями любого целого числа, следовательно, 1 и −1 всегда являются общими делителями любого набора целых чисел. Следовательно, любой набор целых чисел всегда имеет по крайней мере два общих делителя ( 1 и −1 ).

Также нужно отметить, что если целое число b – общий делитель нескольких целых чисел, то противоположное число −b также есть общий делитель данных чисел.

Можно ограничиться лишь положительными делителями (в этом случае все общие делители тоже будут положительными). Такой подход имеет право на существование, но при этом не следует забывать, что каждое целое число, противоположное положительному делителю, также является делителем данного числа.

Наибольший общий делитель (НОД) – определение, обозначение и примеры

Из свойств делимости известно, что если b – делитель целого числа a и a отлично от нуля, то модуль числа b не превосходит модуля числа a . Отсюда следует, что число делителей любого не равного нулю целого числа конечно. Тогда число общих делителей любого набора целых чисел, среди которых хотя бы одно отлично от нуля, тоже конечно. Поэтому из всех общих делителей данных целых чисел мы всегда можем определить наибольшее число (о наибольшем и наименьшем целом числе мы упоминали, когда изучали сравнение целых чисел).

Сейчас и в дальнейшем мы будем подразумевать, что хотя бы одно из данных чисел отлично от нуля. Если все данные числа равны нулю, то их общим делителем является любое целое число, а так как целых чисел бесконечно много, то мы не можем говорить о наибольшем из них. Следовательно, нельзя говорить о наибольшем общем делителе чисел, каждое из которых равно нулю.

Теперь мы можем дать определение наибольшего общего делителя двух чисел.

Наибольший общий делитель двух целых чисел – это наибольшее целое число, делящее два данных целых числа.

Для краткой записи наибольшего общего делителя часто используют аббревиатуру НОД – Наибольший Общий Делитель. Также наибольший общий делитель двух чисел a и b часто обозначают как НОД(a, b) .

Приведем пример наибольшего общего делителя (НОД) двух целых чисел. Наибольший общий делитель чисел 6 и −15 равен 3 . Обоснуем это. Запишем все делители числа шесть: ±6 , ±3 , ±1 , а делителями числа −15 являются числа ±15 , ±5 , ±3 и ±1 . Теперь можно найти все общие делители чисел 6 и −15 , это числа −3 , −1 , 1 и 3 . Так как −3 r₁>r₂>r₃, … – ряд убывающих целых чисел, и этот ряд не может содержать более чем конечное число положительных чисел), тогда r_k – это наибольший общий делитель чисел a и b , то есть, r_k=НОД(a, b) .

Докажем сначала, что r_k является общим делителем чисел a и b , после чего покажем, что r_k не просто делитель, а наибольший общий делитель чисел a и b .

Будем двигаться по записанным равенствам снизу вверх. Из последнего равенства можно сказать, что r_k−1 делится на r_k . Учитывая этот факт, а также предыдущее свойство НОД, предпоследнее равенство r_k−2=r_k−1·q_k+r_k позволяет утверждать, что r_k−2 делится на r_k , так как и r_k−1 делится на r_k и r_k делится на r_k . По аналогии из третьего снизу равенства заключаем, что r_k−3 делится на r_k . И так далее. Из второго равенства получаем, что b делится на r_k , а из первого равенства получаем, что a делится на r_k . Следовательно, r_k является общим делителем чисел a и b .

Осталось доказать, что r_k=НОД(a, b) . Для достаточно показать, что любой общий делитель чисел a и b (обозначим его r₀ ) делит r_k .

Будем двигаться по исходным равенствам сверху вниз. В силу предыдущего свойства из первого равенства следует, что r₁ делится на r₀ . Тогда из второго равенства получаем, что r₂ делится на r₀ . И так далее. Из последнего равенства получаем, что r_k делится на r₀ . Таким образом, r_k=НОД(a, b) .

Из рассмотренного свойства наибольшего общего делителя следует, что множество общих делителей чисел a и b совпадает с множеством делителей наибольшего общего делителя этих чисел. Это следствие из алгоритма Евклида позволяет найти все общие делители двух чисел как делители НОД этих чисел.

Пусть a и b – целые числа, одновременно не равные нулю, тогда существуют такие целые числа u₀ и v₀ , то справедливо равенство НОД(a, b)=a·u₀+b·v₀ . Последнее равенство представляет собой линейное представление наибольшего общего делителя чисел a и b , это равенство называют соотношением Безу, а числа u₀ и v₀ – коэффициентами Безу.

По алгоритму Евклида мы можем записать следующие равенства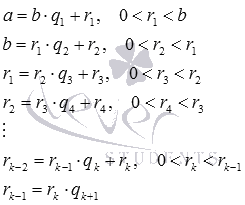

Из первого равенства имеем r₁=a−b·q₁ , и, обозначив 1=s₁ и −q₁=t₁ , это равенство примет вид r₁=s₁·a+t₁·b , причем числа s₁ и t₁ – целые. Тогда из второго равенства получим r₂=b−r₁·q₂= b−(s₁·a+t₁·b)·q₂=−s₁·q₂·a+(1−t₁·q₂)·b . Обозначив −s₁·q₂=s₂ и 1−t₁·q₂=t₂ , последнее равенство можно записать в виде r₂=s₂·a+t₂·b , причем s₂ и t₂ – целые числа (так как сумма, разность и произведение целых чисел является целым числом). Аналогично из третьего равенства получим r₃=s₃·a+t₃·b , из четвертого r₄=s₄·a+t₄·b , и так далее. Наконец, r_k=s_k·a+t_k·b , где s_k и t_k – целые. Так как r_k=НОД(a, b) , и, обозначив s_k=u₀ и t_k=v₀ , получим линейное представление НОД требуемого вида: НОД(a, b)=a·u₀+b·v₀ .

Если m – любое натуральное число, то НОД(m·a, m·b)=m·НОД(a, b) .

Обоснование этого свойства наибольшего общего делителя таково. Если умножить на m обе стороны каждого из равенств алгоритма Евклида, то получим, что НОД(m·a, m·b)=m·r_k , а r_k – это НОД(a, b) . Следовательно, НОД(m·a, m·b)=m·НОД(a, b) .

Пусть p – любой общий делитель чисел a и b , тогда НОД(a:p, b:p)=НОД(a, b):p , в частности, если p=НОД(a, b) имеем НОД(a:НОД(a, b), b:НОД(a, b))=1 , то есть, числа a:НОД(a, b) и b:НОД(a, b) – взаимно простые.

Так как a=p·(a:p) и b=p·(b:p) , и в силу предыдущего свойства, мы можем записать цепочку равенств вида НОД(a, b)=НОД(p·(a:p), p·(b:p))= p·НОД(a:p, b:p) , откуда и следует доказываемое равенство.

Только что доказанное свойство наибольшего общего делителя лежит в основе приведения обыкновенных дробей к несократимому виду.

Сейчас озвучим свойство НОД, которое сводит задачу нахождения наибольшего общего делителя трех и большего количества чисел к последовательному отысканию НОД двух чисел.

Доказательство базируется на следствии из алгоритма Евклида. Общие делители чисел a₁ и a₂ совпадают с делителями d₂ . Тогда общие делители чисел a₁ , a₂ и a₃ совпадают с общими делителями чисел d₂ и a₃ , следовательно, совпадают с делителями d₃ . Общие делители чисел a₁ , a₂ , a₃ и a₄ совпадают с общими делителями d₃ и a₄ , следовательно, совпадают с делителями d₄ . И так далее. Наконец, общие делители чисел a₁, a₂, …, a_k совпадают с делителями d_k . А так как наибольшим делителем числа d_k является само число d_k , то НОД(a₁, a₂, …, a_k)=d_k .

На этом закончим обзор основных свойств наибольшего общего делителя.

Наибольший общий делитель (НОД): определение, примеры и свойства

Эта статья посвящена такому вопросу, как нахождение наибольшего общего делителя. Сначала мы объясним, что это такое, и приведем несколько примеров, введем определения наибольшего общего делителя 2 , 3 и более чисел, после чего остановимся на общих свойствах данного понятия и докажем их.

Что такое общие делители

Чтобы понять, что из себя представляет наибольший общий делитель, сначала сформулируем, что вообще такое общий делитель для целых чисел.

В статье о кратных и делителях мы говорили, что у целого числа всегда есть несколько делителей. Здесь же нас интересуют делители сразу некоторого количества целых чисел, особенно общие (одинаковые) для всех. Запишем основное определение.

Общим делителем нескольких целых чисел будет такое число, которое может быть делителем каждого числа из указанного множества.

Вот примеры такого делителя: тройка будет общим делителем для чисел – 12 и 9 , поскольку верны равенства 9 = 3 · 3 и − 12 = 3 · ( − 4 ) . У чисел 3 и – 12 есть и другие общие делители, такие, как 1 , − 1 и − 3 . Возьмем другой пример. У четырех целых чисел 3 , − 11 , − 8 и 19 будет два общих делителя: 1 и – 1 .

Зная свойства делимости, мы можем утверждать, что любое целое число можно разделить на единицу и минус единицу, значит, у любого набора целых чисел уже будет как минимум два общих делителя.

Также отметим, что если у нас есть общий для нескольких чисел делитель b , то те же числа можно разделить и на противоположное число, то есть на – b . В принципе, мы можем взять лишь положительные делители, тогда все общие делители также будут больше 0 . Такой подход также можно использовать, однако совсем игнорировать отрицательные числа не следует.

Что такое наибольший общий делитель (НОД)

Согласно свойствам делимости, если b является делителем целого числа a , которое не равно 0, то модуль числа b не может быть больше, чем модуль a , следовательно, любое число, не равное 0 , имеет конечное число делителей. Значит, число общих делителей нескольких целых чисел, хотя бы одно из которых отличается от нуля, также будет конечным, и из всего их множества мы всегда можем выделить самое большое число (ранее мы уже говорили о понятии наибольшего и наименьшего целого числа, советуем вам повторить данный материал).

В дальнейших рассуждениях мы будем считать, что хотя бы одно из множества чисел, для которых нужно найти наибольший общий делитель, будет отлично от 0 . Если они все равны 0 , то их делителем может быть любое целое число, а поскольку их бесконечно много, выбрать наибольшее мы не сможем. Иначе говоря, найти наибольший общий делитель для множества чисел, равных 0 , нельзя.

Переходим к формулировке основного определения.

Наибольшим общим делителем нескольких чисел является самое большое целое число, которое делит все эти числа.

На письме наибольший общий делитель чаще всего обозначается аббревиатурой НОД. Для двух чисел его можно записать как НОД ( a , b ) .

Какой можно привести пример НОД для двух целых чисел? Например, для 6 и – 15 это будет 3 . Обоснуем это. Сначала запишем все делители шести: ± 6 , ± 3 , ± 1 , а потом все делители пятнадцати: ± 15 , ± 5 , ± 3 и ± 1 . После этого мы выбираем общие: это − 3 , − 1 , 1 и 3 . Из них надо выбрать самое большое число. Это и будет 3 .

Для трех и более чисел определение наибольшего общего делителя будет почти таким же.

Наибольшим общим делителем трех чисел и более будет самое большое целое число, которое будет делить все эти числа одновременно.

Для чисел a 1 , a 2 , … , a n делитель удобно обозначать как НОД ( a 1 , a 2 , … , a n ) . Само значение делителя записывается как НОД ( a 1 , a 2 , … , a n ) = b .

Приведем примеры наибольшего общего делителя нескольких целых чисел: 12 , – 8 , 52 , 16 . Он будет равен четырем, значит, мы можем записать, что НОД ( 12 , – 8 , 52 , 16 ) = 4 .

Проверить правильность данного утверждения можно с помощью записи всех делителей этих чисел и последующего выбора наибольшего из них.

На практике часто встречаются случаи, когда наибольший общий делитель равен одному из чисел. Это происходит тогда, когда на данное число можно разделить все остальные числа (в первом пункте статьи мы привели доказательство этого утверждения).

Так, наибольший общий делитель чисел 60 , 15 и – 45 равен 15 , поскольку пятнадцать делится не только на 60 и – 45 , но и на само себя, и большего делителя для всех этих чисел не существует.

Особый случай составляют взаимно простые числа. Они представляют собой целые числа с наибольшим общим делителем, равным 1 .

Основные свойства НОД и алгоритм Евклида

У наибольшего общего делителя есть некоторые характерные свойства. Сформулируем их в виде теорем и докажем каждое из них.

Отметим, что данные свойства сформулированы для целых чисел больше нуля, а делители мы рассмотрим только положительные.

Числа a и b имеют наибольший общий делитель, равный НОД для b и a , то есть НОД ( a , b ) = НОД ( b , a ) . Перемена мест чисел не влияет на конечный результат.

Данное свойство следует из самого определения НОД и не нуждается в доказательствах.

Если число a можно разделить на число b , то множество общих делителей этих двух чисел будет аналогично множеству делителей числа b , то есть НОД ( a , b ) = b .

Докажем это утверждение.

Если у чисел a и b есть общие делители, то на них можно разделить любое из них. В то же время если a будет кратным b, то любой делитель b будет делителем и для a , поскольку у делимости есть такое свойство, как транзитивность. Значит, любой делитель b будет общим для чисел a и b . Это доказывает, что если мы можем разделить a на b , то множество всех делителей обоих чисел совпадет с множеством делителей одного числа b . А поскольку наибольший делитель любого числа есть само это число, то наибольший общий делитель чисел a и b будет также равен b , т.е. НОД ( a , b ) = b . Если a = b , то НОД ( a , b ) = НОД ( a , a ) = НОД ( b , b ) = a = b , например, НОД ( 132 , 132 ) = 132 .

Используя это свойство, мы можем найти наибольший общий делитель двух чисел, если одно из них можно разделить на другое. Такой делитель равен одному из этих двух чисел, на которое можно разделить второе число. К примеру, НОД ( 8 , 24 ) = 8 , так как 24 есть число, кратное восьми.

Если верно равенство a = b · q + c (здесь все переменные являются целыми числами), то все общие делители двух чисел a и b будут такими же, как и у чисел b и c , то есть НОД ( a , b ) = НОД ( b , c ) .

Попробуем доказать данное свойство. У нас изначально есть равенство a = b · q + c , и любой общий делитель a и b будет делить и c , что объясняется соответствующим свойством делимости. Поэтому любой общий делитель b и c будет делить a . Значит, множество общих делителей a и b совпадет с множеством делителей b и c , в том числе и наибольшие из них, значит, равенство НОД ( a , b ) = НОД ( b , c ) справедливо.

Следующее свойство получило название алгоритма Евклида. С его помощью можно вычислить наибольший общий делитель двух чисел, а также доказать другие свойства НОД.

Перед тем, как сформулировать свойство, советуем вам повторить теорему, которую мы доказывали в статье о делении с остатком. Согласно ей, делимое число a можно представить в виде b · q + r , причем b здесь является делителем, q – некоторым целым числом (его также называют неполным частным), а r – остатком, который удовлетворяет условию 0 ≤ r ≤ b .

Допустим, у нас есть два целых числа больше 0 , для которых будут справедливы следующие равенства:

a = b · q 1 + r 1 , 0 r 1 b b = r 1 · q 2 + r 2 , 0 r 2 r 1 r 1 = r 2 · q 3 + r 3 , 0 r 3 r 2 r 2 = r 3 · q 4 + r 4 , 0 r 4 r 3 ⋮ r k – 2 = r k – 1 · q k + r k , 0 r k r k – 1 r k – 1 = r k · q k + 1

Эти равенства заканчиваются тогда, когда r k + 1 становится равен 0 . Это случится обязательно, поскольку последовательность b > r 1 > r 2 > r 3 , … представляет собой ряд убывающих целых чисел, который может включать в себя только конечное их количество. Значит, r k является наибольшим общим делителем a и b , то есть, r k = НОД ( a , b ) .

В первую очередь нам надо доказать, что r k – это общий делитель чисел a и b , а после этого – то, что r k является не просто делителем, а именно наибольшим общим делителем двух данных чисел.

Просмотрим список равенств, приведенный выше, снизу вверх. Согласно последнему равенству,
r k − 1 можно разделить на r k . Исходя из этого факта, а также предыдущего доказанного свойства наибольшего общего делителя, можно утверждать, что r k − 2 можно разделить на r k , так как
r k − 1 делится на r k и r k делится на r k .

Третье снизу равенство позволяет нам сделать вывод, что r k − 3 можно разделить на r k , и т.д. Второе снизу – что b делится на r k , а первое – что a делится на r k . Из всего этого заключаем, что r k – общий делитель a и b .

Теперь докажем, что r k = НОД ( a , b ) . Что для этого нужно сделать? Показать, что любой общий делитель a и b будет делить r k . Обозначим его r 0 _.

Просмотрим тот же список равенств, но уже сверху вниз. Исходя из предыдущего свойства, можно заключить, что r 1 делится на r 0 , значит, согласно второму равенству r 2 делится на r 0 . Идем по всем равенствам вниз и из последнего делаем вывод, что r k делится на r 0 . Следовательно, r k = НОД ( a , b ) .

Рассмотрев данное свойство, заключаем, что множество общих делителей a и b аналогично множеству делителей НОД этих чисел. Это утверждение, которое является следствием из алгоритма Евклида, позволит нам вычислить все общие делители двух заданных чисел.

Перейдем к другим свойствам.

Если a и b являются целыми числами, не равными 0 , то должны существовать два других целых числа u 0 и v 0 , при которых будет справедливым равенство НОД ( a , b ) = a · u 0 + b · v 0 .

Равенство, приведенное в формулировке свойства, является линейным представлением наибольшего общего делителя a и b . Оно носит название соотношения Безу, а числа u 0 и v 0 называются коэффициентами Безу.

Докажем данное свойство. Запишем последовательность равенств по алгоритму Евклида:

a = b · q 1 + r 1 , 0 r 1 b b = r 1 · q 2 + r 2 , 0 r 2 r 1 r 1 = r 2 · q 3 + r 3 , 0 r 3 r 2 r 2 = r 3 · q 4 + r 4 , 0 r 4 r 3 ⋮ r k – 2 = r k – 1 · q k + r k , 0 r k r k – 1 r k – 1 = r k · q k + 1

Первое равенство говорит нам о том, что r 1 = a − b · q 1 _. Обозначим 1 = s 1 и − q 1 = t 1 и перепишем данное равенство в виде r 1 = s 1 · a + t 1 · b . Здесь числа s 1 и t 1 будут целыми. Второе равенство позволяет сделать вывод, что r 2 = b − r 1 · q 2 = b − ( s 1 · a + t 1 · b ) · q 2 = − s 1 · q 2 · a + ( 1 − t 1 · q 2 ) · b . Обозначим − s 1 · q 2 = s 2 и 1 − t 1 · q 2 = t 2 и перепишем равенство как r 2 = s 2 · a + t 2 · b , где s 2 и t 2 также будут целыми. Это объясняется тем, что сумма целых чисел, их произведение и разность также представляют собой целые числа. Точно таким же образом получаем из третьего равенства r 3 = s 3 · a + t 3 · b , из следующего r 4 = s 4 · a + t 4 · b и т.д. В конце заключаем, что r k = s k · a + t k ·b при целых s k и t k . Поскольку r k = НОД ( a , b ) , обозначим s k = u 0 и t k = v 0 , В итоге мы можем получить линейное представление НОД в требуемом виде: НОД ( a , b ) = a · u 0 + b · v 0 .

НОД ( m · a , m · b ) = m · НОД ( a , b ) при любом натуральном значении m .

Обосновать это свойство можно так. Умножим на число m обе стороны каждого равенства в алгоритме Евклида и получим, что НОД ( m · a , m · b ) = m · r k , а r k – это НОД ( a , b ) . Значит, НОД ( m · a , m · b ) = m ·НОД ( a , b ) . Именно это свойство наибольшего общего делителя используется при нахождении НОД методом разложения на простые множители.

Если у чисел a и b есть общий делитель p , то НОД ( a : p , b : p ) = НОД ( a , b ) : p . В случае, когда p = НОД ( a , b ) получим НОД ( a : НОД ( a , b ) , b : НОД ( a , b ) = 1 , следовательно, числа a : НОД ( a , b ) и b : НОД ( a , b ) являются взаимно простыми.

Поскольку a = p · ( a : p ) и b = p · ( b : p ) , то, основываясь на предыдущем свойстве, можно создать равенства вида НОД ( a , b ) = НОД ( p · ( a : p ) , p · ( b : p ) ) = p ·НОД ( a : p , b : p ) , среди которых и будет доказательство данного свойства. Это утверждение мы используем, когда приводим обыкновенные дроби к несократимому виду.

Наибольшим общим делителем a 1 , a 2 , … , a k будет число d k , которое можно найти, последовательно вычисляя НОД ( a 1 , a 2 ) = d 2 , НОД ( d 2 , a 3 ) = d 3 , НОД ( d 3 , a 4 ) = d 4 , … , НОД ( d k – 1 , a k ) = d k .

Это свойство полезно при нахождении наибольшего общего делителя трех и более чисел. С помощью него можно свести это действие к операциям с двумя числами. Его основой является следствие из алгоритма Евклида: если множество общих делителей a 1 , a 2 и a 3 совпадает с множеством d 2 и a 3 , то оно совпадет и с делителями d 3 . Делители чисел a 1 , a 2 , a 3 и a 4 совпадут с делителями d 3 , значит, они совпадут и с делителями d 4 , и т.д. В конце мы получим, что общие делители чисел a 1 , a 2 , … , a k совпадут с делителями d k , а поскольку наибольшим делителем числа d k будет само это число, то НОД ( a 1 , a 2 , … , a k ) = d k .

Это все, что мы хотели бы рассказать о свойствах наибольшего общего делителя.

Наибольший общий делитель

Наибольшим общим делителем (НОД) для двух целых чисел m и n называется наибольший из их общих делителей. [1] Пример: для чисел 70 и 105 наибольший общий делитель равен 35.

Наибольший общий делитель существует и однозначно определён, если хотя бы одно из чисел m или n не ноль.

Возможные обозначения наибольшего общего делителя чисел m и n:

Понятие наибольшего общего делителя естественным образом обобщается на наборы из более чем двух целых чисел.

Содержание

Связанные определения

Наименьшее общее кратное

Наименьшее общее кратное (НОК) двух целых чисел m и n — это наименьшее натуральное число, которое делится на m и n. Обозначается НОК(m,n) или , а в английской литературе lcm(m,n).

НОК для ненулевых чисел m, n всегда существует и связан с НОД следующим соотношением:

Это частный случай более общей теоремы: если — ненулевые числа, D — какое-либо их общее кратное, то имеет место формула:

Взаимно простые числа

Числа m и n называются взаимно-простыми, если у них нет общих делителей, кроме единицы. Для таких чисел НОД(m,n) = 1. Обратно, если НОД(m,n) = 1, то числа взаимно просты.

Аналогично, целые числа , где , называются взаимно простыми, если их наибольший общий делитель равен единице.

Следует различать понятия взаимной простоты, когда НОД набора чисел равен 1, и попарной взаимной простоты, когда НОД равен 1 для каждой пары чисел из набора. Из попарной простоты вытекает взаимная простота, но не наоборот. Например, НОД(6,10,15) = 1, но любые пары из этого набора не взаимно просты.

Способы вычисления

Эффективными способами вычисления НОД двух чисел являются алгоритм Евклида и бинарный алгоритм.

Кроме того, значение НОД(m,n) можно легко вычислить, если известно каноническое разложение чисел m, n на простые множители:

где — различные простые числа, а и — неотрицательные целые числа (они могут быть нулями, если соответствующее простое отсутствует в разложении). Тогда НОД(m,n) и НОК(m,n) выражаются формулами:

Если чисел более двух: , их НОД находится по следующему алгоритму:

……… — это и есть искомый НОД.

Свойства

• Основное свойство: наибольший общий делитель m и n делится на любой общий делитель этих чисел. Пример: для чисел 12 и 18 наибольший общий делитель равен 6; он делится на все общие делители этих чисел: 1, 2, 3, 6.
  • Следствие 1: множество общих делителей m, n совпадает с множеством делителей НОД(m, n).
  • Следствие 2: множество общих кратных m, n совпадает с множеством кратных НОК(m, n).
• Если m делится на n, то НОД(m, n) = n. В частности, НОД(n, n) = n.
• — общий множитель можно выносить за знак НОД.
• Если , то после деления на D числа становятся взаимно простыми, то есть, . Это означает, в частности, что для приведения дроби к несократимому виду надо разделить её числитель и знаменатель на их НОД.
• Мультипликативность: если взаимно просты, то:

• Наибольший общий делитель чисел m и n может быть определён как наименьший положительный элемент множества всех их линейных комбинаций:

и поэтому (m,n) представим в виде линейной комбинации чисел m и n: . Это соотношение называется соотношением Безу, а коэффициенты u и v — коэффициентами Безу. Коэффициенты Безу эффективно вычисляются расширенным алгоритмом Евклида. Это утверждение обобщается на наборы натуральных чисел — его смысл в том, что подгруппа группы, порождённая набором , — циклическая и порождается одним элементом: НОД.

Вариации и обобщения

Понятие делимости целых чисел естественно обобщается на произвольные коммутативные кольца, такие, как кольцо многочленов (англ.) или гауссовы целые числа. Однако, определить НОД(a, b) как наибольший из общих делителей a, b нельзя, так как в таких кольцах, вообще говоря, не определено отношение порядка. Поэтому в качестве определения НОД берётся его основное свойство:

наибольшим общим делителем НОД(a, b) называется тот общий делитель, который делится на все остальные общие делители a и b.

Для натуральных чисел новое определение эквивалентно старому. Для целых чисел НОД в новом смысле уже не однозначен: противоположное ему число тоже будет НОД. Для гауссовых чисел число НОД возрастает до 4.

НОД двух элементов коммутативного кольца, вообще говоря, не обязан существовать. Например, для нижеследующих элементов a, b кольца не существует наибольшего общего делителя:

В евклидовых кольцах наибольший общий делитель всегда существует и определён с точностью до делителей единицы, то есть количество НОД равно числу делителей единицы в кольце.

Источники:

http://www.cleverstudents.ru/divisibility/nod.html
http://zaochnik.com/spravochnik/matematika/delimost/naibolshij-obschij-delitel-nod/
http://dik.academic.ru/dic.nsf/ruwiki/8719