Что значит делитель и кратное. Делители и кратные числа

Делители и кратные числа: определения и примеры

Эта статья посвящена делителям и кратным. Здесь мы объясним данные понятия, сформулируем определения, приведем примеры делителей и различных кратных чисел (рассмотрим пока только целые числа). Отдельно остановимся на делителях 1 и – 1 , а также делителях и кратных 0 .

Основные определения

Для начала сформулируем определения для целого числа.

Делитель целого числа a есть такое число b , на которое можно разделить a без остатка.

Если вспомнить такое понятие, как делимость, то данную формулировку можно слегка изменить.

Делитель целого числа a – это такое число b , которое в сочетании с некоторым числом q делает справедливым равенство a = b · q .

Когда мы говорим о числе b , являющимся делителем целого числа a , это значит, что b делит a , что можно записать кратко как b | a или b a .

Согласно определению целых чисел, а также свойствам умножения целых чисел, любое целое число можно разделить на единицу и на себя, то есть a = a · 1 и a = 1 · a . Зная свойства умножения, мы можем также вывести равенства a = ( − a ) · ( − 1 ) и a = ( − 1 ) · ( − a ) . Из них следует, что у a будет еще два делителя, равных − a и − 1 . Следовательно, целое число a мы всегда можем разделить на a , − a , 1 и − 1 . К примеру, число 12 делится на 12 , – 12 , 1 и – 1 .

Остановимся на делителях таких чисел, как нуль, единица и минус единица. Поскольку нам знакомы свойства делимости, то мы можем заключить, что делителем 0 может стать любое целое число (включая сам 0 ), а единица и минус единица имеют только делители, равные 1 и − 1 соответственно.

Таким образом, 0 всегда будет иметь бесконечно большое число делителей в виде целых чисел (сюда входит и нуль), а у 1 и − 1 будут только 2 делителя – единица и минус единица. Минимальное количество делителей для любого целого числа a равно четырем. В их число входят a , − a , 1 и − 1 .

Какие еще можно привести примеры делителей в случае с целыми числами?

Так, 8 можно разделить на – 2 , поскольку равенство 8 = ( − 2 ) · ( − 4 ) верное (если нужно, повторите материал об умножении целых чисел). Восьмерку мы также можем разделить на − 8 , − 4 , − 1 , 1 , 2 , 4 , 8 , а вот – 3 не входит в состав делителей, поскольку числа q , при котором равенство 8 = ( − 3 ) · q было бы верным, не существует. То есть разделить 8 на – 3 мы можем только с остатком. Кроме указанных делителей, мы не можем разделить восьмерку ни на какие целые числа без остатка.

Рассмотренные выше примеры говорят нам о том, что в качестве делителей целого числа могут выступать не только положительные, но и отрицательные целые числа. Эта возможность обоснована одним из свойств делимости: если b – делитель целого числа a , то и противоположное число – b тоже будет его делителем. Следовательно, можно разбирать только случаи с положительными делителями и просто распространять полученные результаты на отрицательные.

Вспомним также и другое свойство делимости, которое гласит, что если целое число b будет делителем a , то a можно разделить и на – b , следовательно, множества делителей для положительного и отрицательного a будут совпадать. Это правило опять же подтверждает возможность работы только с положительными числами для простоты и краткости вычислений.

Далее мы будем говорить лишь о положительных делителях целых положительных (натуральных) чисел.

У единицы есть только один положительный делитель – сама единица. Этим 1 отличается от остальных натуральных чисел, поскольку другие имеют не меньше 2 делителей: кроме единицы их можно разделить на числа, равные им самим. В зависимости от того, имеются ли делители, отличные от самого числа и единицы, различают числа простые и составные.

Наименьший положительный делитель числа a – это единица (если само число a не равно 1 ),
а число a – наибольший положительный делитель самого себя (подробнее о сравнении трех и более натуральных чисел мы писали в отдельной статье). Таким образом, для любого натурального a положительный делитель b будет соответствовать условию 1 ≤ b ≤ a . Важную роль здесь также играет наибольший общий делитель (НОД), о котором мы поговорим отдельно.

Понятие кратных чисел

Начнем, как всегда, с определения.

Число a называется кратным b , если его можно разделить на b без остатка.

Другими словами, кратное b число является некоторым числом a , для которого будет верным равенство a = b · q (здесь q – некоторое целое число). Если у нас есть a , которое по отношению к b является кратным, мы говорим, что a кратно b . Записать это можно так: a ⋮ b .

Между кратным и делимым существует вполне определенная связь. На самом деле, если a является кратным b , то b будет делителем данного числа, и наоборот.

Возьмем несколько примеров кратных чисел.

Так, – 12 будет кратно трем, поскольку − 12 = 3 · ( − 4 ) . У тройки есть много других кратных, например, 0 , 3 , − 3 , 6 , − 6 , 9 , − 9 и др. А 5 не будет кратным 3 , поскольку нет такого q , при котором было бы верным равенство 7 = 3 · q .

Согласно определению кратных чисел, 0 будет кратным по отношению к любому b , в том числе и нулевому. Доказательством является равенство 0 = b · 0 , ведь умножение любого числа на нуль дает в итоге нуль.

Также уточним, что для любого целого числа b существует бесконечно много кратных, и любое целое число, соответствующее произведению b · q , где q – любое целое число, будет кратным b .

Наименьшее положительное кратное положительного числа есть само это число. Обратите внимание, что наименьшее кратное в этом случае не нужно путать с наименьшим общим кратным для нескольких чисел (НОК).

Далее будут рассмотрены другие случаи с натуральными кратными целых положительных чисел.

Делители и кратные числа

Тема «Кратные числа» изучается в 5 классе общеобразовательной школы. Ее целью является совершенствование письменных и устных навыков математических вычислений. На этом уроке вводятся новые понятия – «кратные числа» и «делители», отрабатывается техника нахождения делителей и кратных натурального числа, умение находить НОК различными способами.

Эта тема является очень важной. Знания по ней можно применить при решении примеров с дробями. Для этого нужно найти общий знаменатель путем расчета наименьшего общего кратного (НОК).

Кратным А считается целое число, которое делится на А без остатка.

Каждое натуральное число имеет бесконечное количество кратных ему чисел. Наименьшим считается оно само. Кратное не может быть меньше самого числа.

Нужно доказать, что число 125 кратно числу 5. Для этого нужно первое число разделить на второе. Если 125 делится на 5 без остатка, то ответ положительный.

Все натуральные числа можно разделить на 1. Кратное является делителем для себя самого.

Как мы знаем, числа при делении называются «делимое», «делитель», «частное».

где 27 – делимое, 9 – делитель, 3 – частное.

Числа, кратные 2, – это те, которые при делении на два не образуют остатка. К ним относятся все четные.

Числа, кратные 3, – это такие, которые без остатка делятся на 3 (3, 6, 9, 12, 15…).

Например, 72. Это число кратно числу 3, потому что делится на 3 без остатка (как известно, число делится на 3 без остатка, если сумма его цифр делится на 3)

Является ли число 11 кратным 4?

Ответ: не является, так как есть остаток.

Общее кратное двух или более целых чисел – это такое, которое делится на эти числа без остатка.

Для каждого числа необходимо отдельно выписать в строку кратные числа – вплоть до нахождения одинакового.

Данный способ применим для небольших чисел.

При расчёте НОК встречаются особые случаи.

1. Если необходимо найти общее кратное для 2-х чисел (например, 80 и 20), где одно из них (80) делится без остатка на другое (20), то это число (80) и есть наименьшее кратное этих двух чисел.

2. Если два простых числа не имеют общего делителя, то можно сказать, что их НОК – это произведение этих двух чисел.

Рассмотрим последний пример. 6 и 7 по отношению к 42 являются делителями. Они делят кратное число без остатка.

В этом примере 6 и 7 являются парными делителями. Их произведение равно самому кратному числу (42).

Число называется простым, если делится только само на себя или на 1 (3:1=3; 3_3=1). Остальные называются составными.

В другом примере нужно определить, является ли 9 делителем по отношению к 42.

Ответ: 9 не является делителем числа 42, потому что в ответе есть остаток.

Делитель отличается от кратного тем, что делитель – это то число, на которое делят натуральные числа, а кратное само делится на это число.

Наибольший общий делитель чисел a и b, умноженный на их наименьшее кратное, даст произведение самих чисел a и b.

А именно: НОД (а, b) х НОК (а, b) = а х b.

Общие кратные числа для более сложных чисел находят следующим способом.

Например, найти НОК для 168, 180, 3024.

Эти числа раскладываем на простые множители, записываем в виде произведения степеней:

Дальше выписываем все представленные основания степеней с самыми большими показателями и перемножаем их:

Делители и кратные числа, определения и примеры.

В этой статье мы обсудим делители и кратные. Здесь мы дадим определения делителя и кратного числа. Эти определения нам позволят привести примеры делителей и кратных различных целых чисел. Отдельно рассмотрим делители единицы и минус единицы, а также поговорим о делителях и кратных нуля.

Навигация по странице.

Делители числа – определение, примеры

Сначала дадим определение делителя целого числа.

Делителем целого числа a называется целое число b , на которое a делится нацело.

Если обратиться к понятию делимости, то озвученному определению делителя можно дать иную формулировку.

Целое число b называется делителем целого числа a , если существует такое целое число q , что справедливо равенство a=b·q .

Если целое число b является делителем целого числа a , то говорят, что b делит a , при этом используют краткую запись вида b|a (встречается также обозначение ba ).

Из определения делителя целого числа и свойств умножения целых чисел следует, что любое целое число делится на себя и на единицу, так как a=a·1 и a=1·a . На основании свойств умножения целых чисел можно записать равенства a=(−a)·(−1) и a=(−1)·(−a) , из которых следует, что числа −a и −1 также являются делителями целого числа a . Таким образом, числа a , −a , 1 и −1 всегда являются делителями целого числа a . Например, делителями числа 15 являются числа 15 , −15 , 1 и −1 .

Отдельно нужно сказать о делителях целых чисел 0 , 1 и −1 . Вспомнив свойства делимости, заключаем, что делителем нуля является любое целое число, в том числе и нуль, а делителями единицы и минус единицы являются только числа 1 и −1 .

Итак, целое число 0 имеет бесконечно много делителей, ими являются любые целые числа, числа 1 и −1 имеют только два делителя – единицу и минус единицу, а любое другое целое число a (кроме −1 , 0 и 1 ) имеет, по крайней мере, четыре делителя: a , −a , 1 и −1 .

Приведем еще примеры делителей целых чисел. Число −2 является делителем числа 8 , так как верно равенство 8=(−2)·(−4) (при необходимости смотрите статью умножение целых чисел, правила, примеры). Делителями целого числа 8 являются также числа −8 , −4 , −1 , 1 , 2 , 4 , 8 . А вот число −3 не является делителем числа 8 , так как не существует целого числа q такого, чтобы выполнялось условие 8=(−3)·q . Иными словами, возможно только деление с остатком целых чисел 8 и −3 . Вообще, ни одно целое число, кроме −8 , −4 , −2 , −1 , 1 , 2 , 4 , 8 , не является делителем 8 .

Из рассмотренных примеров отчетливо видно, что делителями целого числа могут быть как целые положительные, так и целые отрицательные числа. Это утверждение обосновывается следующим свойством делимости: если целое число b является делителем целого числа a , то −b ( b и −b – противоположные числа) также является делителем числа a . Таким образом, мы можем рассматривать лишь положительные делители чисел, но при этом помнить, что все целые числа, противоположные положительным делителям данного числа, также являются делителями этого числа.

Напомним еще одно свойство делимости: если целое число b является делителем целого числа a , то b также является делителем целого числа −a . Из него следует, что множества делителей чисел a и −a совпадают. Поэтому, отдавая дань краткости и простоте, мы будем рассматривать лишь делители целых положительных чисел.

Учитывая информацию двух предыдущих абзацев, дальше можно рассматривать лишь положительные делители целых положительных чисел (натуральных чисел).

Натуральное число 1 имеет единственный положительный делитель – это число 1 . Этот факт отличает единицу от других натуральных чисел, так как натуральные числа, отличные от единицы, имеют не менее двух делителей, а именно себя самого и 1 . В зависимости от отсутствия или наличия делителей, отличных от самого натурального числа и от единицы, различают простые и составные числа.

Единица является наименьшим положительным делителем натурального числа a , отличного от 1 , а само число a является наибольшим положительным делителем (о наибольшем и наименьшем числе мы говорили в разделе сравнение трех и большего количества натуральных чисел). То есть, для любого натурального числа a любой его положительный делитель b удовлетворяет условию .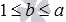

Здесь же заметим, что особую роль имеет наибольший общий делитель – НОД.

Кратные числа – определение, примеры

Дадим определение кратного.

Источники:

http://zaochnik.com/spravochnik/matematika/delimost/deliteli-i-kratnye-chisla/
http://fb.ru/article/100205/deliteli-i-kratnyie-chisla
http://www.cleverstudents.ru/divisibility/divisors_and_multiples.html