Воздушное и открытое пространство. Примеры геометрических фигур в многомерном евклидовом пространстве
Евклидовы пространства
Определение евклидова пространства
Вещественное линейное пространство [math]mathbb
0quad forall mathbf
forall lambdain mathbb
В скалярном произведении [math]langlemathbf, mathbf
Линейные операции над векторами евклидова пространства удовлетворяют аксиомам 1–8 линейного пространства, а операция скалярного умножения векторов удовлетворяет аксиомам 1–4 скалярного произведения. Можно сказать, что евклидово пространство — это вещественное линейное пространство со скалярным произведением. Поскольку евклидово пространство является линейным пространством, на него переносятся все понятия, определенные для линейного пространства, в частности, понятия размерности и базиса.
Простейшие следствия из аксиом скалярного произведения
1. Аксиомы 2 и 3 скалярного произведения можно заменить одним условием линейности скалярного произведения по первому сомножителю:
forall alpha,betain mathbb
2. Условие линейности скалярного произведения по первому сомножителю в силу симметричности (аксиома 1) справедливо и для второго сомножителя, т.е. скалярное произведение линейно по любому сомножителю.
3. Линейность скалярного произведения по любому сомножителю распространяется на линейные комбинации векторов:
для любых векторов [math]mathbf_i,,mathbf
4. Если хотя бы один сомножитель — нулевой вектор, то скалярное про изведение равно нулю:
Действительно, представим нулевой вектор в виде [math]mathbf
Неравенство Коши-Буняковского
Для любых векторов [math]mathbf[/math] и [math]mathbf
В самом деле, для любого действительного числа [math]lambda[/math] и любых векторов [math]mathbf[/math] и [math]mathbf
Следовательно, дискриминант квадратного трехчлена (переменной [math]lambda[/math] ) не больше нуля, т.е. [math]4 langle mathbf,mathbf
Примеры евклидовых пространств
Определяя для элементов линейного пространства операцию скалярного произведения, получаем евклидово пространство. Если скалярное произведение можно ввести разными способами в одном и том же линейном пространстве, то и получаемые евклидовы пространства будут разными. Приведем примеры евклидовых пространств, соответствующих рассмотренным ранее примерам линейных пространств.
1. В нулевом линейном пространстве [math]
2. В пространствах [math]V_1,,V_2,,V_3[/math] векторы (свободные или радиус- векторы) рассматриваются как направленные отрезки. В курсе элементарной геометрии вводятся понятия длины вектора и величины угла между векторами, а затем определяется скалярное произведение: [math]langle vec,vec
3. В пространстве [math]mathbb
где [math]A[/math] — квадратная симметрическая положительно определенная матрица n-го порядка. Проверим выполнение аксиом 1-4. Аксиома 1 (симметричность) выполняется в силу симметричности матрицы [math]A:[/math] [math]langle x,yrangle= x^TAy= y^TA^Tx= y^TAx= langle y,xrangle[/math] , поскольку число при транспонировании не изменяется, т.е. [math]x^TAy=y^TA^Tx[/math] . Свойство линейности по первому сомножителю (см. п.1 простейших следствий из аксиом) для (8.26) выполняется:
Значит, выполняются аксиомы 2 и 3. Аксиома 4 также выполняется, так как квадратичная форма [math]langle x,xrangle= x^TAx[/math] положительно определенная. Таким образом, пространство [math]mathbb
Это скалярное произведение считается стандартным в пространстве [math]mathbb
Приведем примеры формул, которые не задают скалярного произведения в [math]mathbb
1) [math]langle x,yrangle= |x_1|cdot|y_1|+|x_2|cdot|y_2|[/math] — аксиомы 1, 4 выполняются, а аксиомы 2, 3 — нет;
2) [math]langle x,yrangle=x_2cdot y_2[/math] — аксиомы 1, 2, 3 выполняются, а аксиома 4 — нет.
4. Пространство [math]
5. В пространстве [math]C[a,b][/math] действительных функций, определенных и непрерывных на данном промежутке [math][a,b][/math] , скалярное произведение можно задать формулой:
Таким образом, пространство [math]C[a,b][/math] со скалярным произведением (8.28) является евклидовым. Скалярное произведение (8.28) считается стандартным в пространстве [math]C[a,b][/math] . Для разрывных функций формула (8.28) не определяет скалярного произведения, так как нарушается аксиома 4. Неравенство (8.25) Коши-Буняковского в пространстве [math]C[a,b][/math] со скалярным произведением (8.28) трансформируется в неравенство Шварца :
6. В пространстве [math]P(mathbb
В пространстве [math]P_n(mathbb
Выражение в правой части (8.29) симметрично для коэффициентов двух многочленов, поэтому аксиома 1 выполняется. Аксиомы 2, 3 следуют из линейности выражения по коэффициентам каждого многочлена. Проверим аксиому 4. Запишем скалярный квадрат [math]langle p,prangle= a_n^2+ldots+ a_1^2+ a_0^2geqslant0[/math] . Заметим, что [math]langle p,prangle=0[/math] только при [math]a_n=ldots=a_1=a_0=0[/math] , т.е. в случае нулевого много члена [math]p(x)equiv0[/math] . Следовательно, формула (8.29) задает скалярное произведение в пространстве [math]P_n(mathbb
В пространстве [math]P_3(mathbb
В силу симметричности и линейности правой части (8.30) по значениям многочленов, заключаем, что аксиомы 1-3 выполняются. Проверим выполнение аксиомы 4. Приравняв скалярный квадрат нулю, получаем
Это возможно только при [math]p(1)=p(2)=p(3)=0[/math] . Из этих трех равенств не следует, однако, что многочлен [math]p(x)[/math] нулевой. Например, ненулевой многочлен [math]p(x)=(x-1)(x-2)(x-3)[/math] удовлетворяет трем равенствам. Следовательно, в пространстве [math]P_3(mathbb
Длина вектора и угол между векторами в евклидовом пространстве
Длиной (нормой) вектора [math]mathbf
Имея в виду обозначение, длину [math]|mathbf
Углом между ненулевыми векторами [math]mathbf[/math] и [math]mathbf
Представив неравенство Коши-Буняковского (8.25) в виде [math]bigl|langle mathbf,mathbf
Длина вектора и угол между векторами называются основными метрическими понятиями .
Из неравенства Коши-Буняковского (8.25) следует неравенство треугольника :
Докажем последнее неравенство. Применяя оценку [math]langle mathbf,mathbf
то есть [math]|mathbf+mathbf
Пример 8.17. Даны векторы евклидовых пространств:
y=begin
y=begin
g(x)=cos
q(x)=x+2[/math] — элементы пространства [math]P_2(mathbb
q(x)=x+2[/math] — элементы пространства [math]P_2(mathbb
В каждом пространстве найти длины двух данных векторов и угол между ними.
Решение. а) Находим скалярные произведения:
б) Находим скалярные произведения:
в) Находим скалярные произведения:
г) Находим скалярные произведения:
langle p,qrangle= 1!cdot!0+(-2)!cdot!1+1!cdot!2=0;
langle q,qrangle= 0!cdot!0+1!cdot!1+2!cdot!2=5.[/math]
д) Находим скалярные произведения:
langle p,qrangle= 0!cdot!3+1!cdot!4+4!cdot!5=24;
langle q,qrangle= 3!cdot!3+4!cdot!4+5!cdot!5=50.[/math]
Арифметическая модель многомерного евклидова пространства
Мы отмечали в п.2.3, §2, что аксиоматика Д. Гилберта не может быть обобщена для построения модели геометрии высоких размерностей в мыслимом многомерном евклидовом пространстве. Обратимся к схеме Г.Вейля, согласно которой строилось арифметическое пространство R 3 . На самом деле эта схема не зависит от размерности вспомогательного векторного пространства Е n . При n=2 и n=3 она просто одна и та же и отличается набором координат. В случае «мыслимой» многомерной геометрии операция откладывания вектора (1) является формальным определением множества точек арифметического n-мерного евклидова пространства R n , а в остальном схема построения R n при n>3 такова же, как и при n£3 и состоит в реализации следующих трёх групп аксиом.
1.Группа аксиом векторного пространства. Эта группа включает восемь аксиом векторного пространства, сформулированных в п. 3.1 §3 и дополнительную девятую аксиому размерности, сформулированную в п. 3.2 §3. Эти аксиомы определяют арифметическую модель Е n n-мерного векторного пространства, см. п. 3.3 §3.
2 .Аксиомы скалярного произведения.
Сюда входят три аксиомы 1) – 3) в формуле ( 5), приведенные в виде свойств в п.3.4 §3.
3. Аксиомы откладывания векторов.
Эта группа аксиом состоит из трех свойств операции откладывания векторов, определенной в начале этого параграфа.
Вывод 3.
Система аксиом Г. Вейля определяет абстрактное n-мерное арифметическое евклидово пространство R n , в котором основные геометрические объекты – точки, прямые, плоскости размерности 2, 3, . n-1 – задаются системами алгебраических уравнений. При n>3 отсутствует «геометрическая модель» евклидова пространства, отождествляемая с реальными объектами .Например объектами четырёхмерного арифметического пространства R 4 являются лишь мыслимые объекты, представляемые арифметической моделью и «несущие геометрические свойства» по аналогии с R 3 . Именно поэтому для определения координат точек «мыслимого» многомерного евклидова пространства требуется аксиома 3 – существования хотя бы одной точки O, для которой определена операция откладывания векторов из E 4 и которая считается началом координат в R 4 : O (0,0,0,0)ÎR 4 .
Замечание о схеме Г.Вейля.
Способ построения декартовой системы координат на плоскости и в пространстве известен всем из школьного курса математики. Этот способ состоит из изображения трёх взаимно перпендикулярных числовых осей OX, OY, OZ пересекающихся в общей точке О, которая является началом координат. Координатами точки М евклидова пространства считается упорядоченная тройка чисел ( x, y, z), которая получается в результате ортогональной проекции точки М на координатные оси. Такой способ построения координат опирается на наше визуальное представление и не может быть использован для построения арифметической модели многомерного пространства. Гениальность схемы Г.Вейля заключается в том, что операцию построения координат в двухмерном и трёхмерном случаях он представил как интеллектуальную операцию и эту операцию он реализовал тремя аксиомами откладывания вектора. Эти три аксиомы не зависят от размерности векторного пространства и с использованием структуры векторного пространства и скалярного произведения позволяют построить многомерную координатную модель евклидова пространства .
Аксиоматическое обоснование евклидовой геометрии по Вейлю – наиболее распространенная схема построения арифметической модели R n , применяемой в задачах линейного программирования, исследования операций и других задачах физики, математики, информатики и естествознания.
4.3. Вопросы и задания к теме «Модель Вейля евклидовой геометрии»
Вопросы.
1.Какие аксиомы позволяют вычислять длины отрезков и углы в многомерной геометрии?
2. Чем отличается аксиоматика Вейля трёхмерного евклидова пространства от многомерного?
3. Как задаются точки в модели Вейля? Как задаются координатные плоскости?
4. Как задаются плоскости в модели Вейля?
Задания.
1. Сформулируйте аксиоматику Вейля многомерной евклидовой геометрии.
2. Дайте геометрическую интерпретацию аксиомам Вейля 1 – 3.
3. Задайте следующие геометрические объекты в модели Вейля:
– шар и сфера в трёхмерном пространстве;
– шар и сфера в многомерном пространстве.
4. Постройте примеры других геометрических объектов.

Папиллярные узоры пальцев рук – маркер спортивных способностей: дерматоглифические признаки формируются на 3-5 месяце беременности, не изменяются в течение жизни.
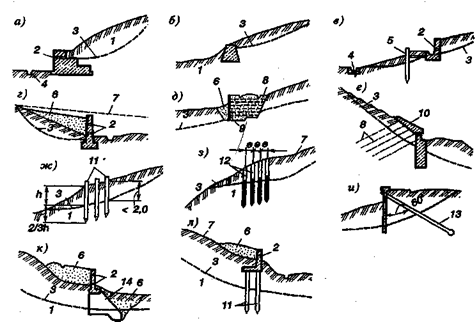
Механическое удерживание земляных масс: Механическое удерживание земляных масс на склоне обеспечивают контрфорсными сооружениями различных конструкций.

Поперечные профили набережных и береговой полосы: На городских территориях берегоукрепление проектируют с учетом технических и экономических требований, но особое значение придают эстетическим.
Геометрические фигуры в пространстве
С пространственными геометрическими фигурами (куб, шар, параллелепипед и др.) дети знакомятся в практической деятельности (при конструировании, во время игры) гораздо раньше, чем с плоскими фигурами. Особенности мышления младших дошкольников определяют выбор наглядного материала. В этом возрасте важно, чтобы изучаемый объект был крупный, яркий, чтобы им можно было выполнять действия (поиграть). Обследование идет на сенсорной основе, поэтому с моделями объемных фигур детям знакомиться легче. Кубики, шарики, бруски и др. входят в игру детей одновременно с первыми игрушками. Обычно математические названия им не даются, но идет знакомство с различными объемными формами, а в речь вводятся только некоторые термины.
Основными фигурами в пространстве считаются: точка, прямая, плоскость. На каждой плоскости выполняются все утверждения планиметрии. В стереометрии, так же как в планиметрии, вводится ряд аксиом, которые изучаются в школьном курсе геометрии.
Объемные геометрические фигуры называют геометрическими телами. В пространстве выделяют многогранники (призма, пирамида и др.) и тела вращения (шар, конус, цилиндр и др.).
Многогранники
Многогранник– это ограниченное тело, поверхность которого состоит из конечного числа многоугольников. Эти многоугольники называются гранями, их стороны — ребрами, а вершины – вершинами многогранника.
Многогранник называется выпуклым, если он расположен по одну сторону от плоскости любой его грани (рис. 70).
Выпуклый многогранник невыпуклый многогранник

Задание 43
Покажите вершины, ребра и грани многогранников, изображенных на рисунке 70. Какими геометрическими фигурами они являются!
Правильный выпуклый многогранник имеет грани – правильные равные многоугольники, и в каждой его вершине сходится одинаковое число ребер.
Задание 44
1. Вспомните, какие фигуры называют равными.
2. Назовите известные вам правильные выпуклые многогранники.
 Всего существует 5 правильных многогранников, в отличие от правильных многоугольников, которых бесконечно много. Это обусловлено двумя причинами:
Всего существует 5 правильных многогранников, в отличие от правильных многоугольников, которых бесконечно много. Это обусловлено двумя причинами:

Прямоугольный параллелепипед – это параллелепипед, все грани которого прямоугольники (рис. 75).
Куб — это прямоугольный параллелепипед с равными ребрами (или все грани которого являются квадратами) (рис. 76).
Дошкольники, изучая куб, могут отметить, что его поверхность состоит из шести квадратов, что у него 8 вершин. Свойства куба осваиваются ими, например, при выполнении такого задания: «Обклей кубик цветной бумагой. Что для этого нужно?» (вырезать 6 одинаковых квадратов).
Прямоугольный параллелепипед в детском саду часто называют «кирпичиком» или «бруском», что допустимо в предматематической подготовке. Эти слова являются предэталонными названиями геометрических фигур, так же как «кубик», «крыша» (треугольная призма), «столбик» (цилиндр) и др.
Младшим школьникам можно предложить задание: «Вырежи выкройку для коробки. Какую форму имеет каждая часть?» Таким образом, дети выясняют, что гранями прямоугольного параллелепипеда являются прямоугольники, не формулируя этого явно.
Пирамида — многогранник, состоящий из плоского многоугольника (основания), точки, не лежащей в плоскости основания (вершины), и всех отрезков, соединяющих вершину пирамиды с точками основания (рис. 77). Отрезки, соединяющие вершину пирамиды с вершинами основания, называются боковыми ребрами. Поверхность пирамиды состоит из основания и боковых граней. Все боковые граны — треугольники.
В зависимости от числа углов многоугольника, являющегося основанием, пирамиды бывают: треугольные (рис. 77а), четырехугольные (рис. 776), пятиугольные и другие пирамиды.

Любая грань треугольной пирамиды может служить ее основанием. Это же название носит и правильный многогранник, тетраэдр, гранями которого являются равные равносторонние треугольники.
Форму тетраэдра имеет пакет молока (старой упаковки), а египетские пирамиды имеют форму четырехугольной правильной пирамиды. Дошкольники называют «пирамидкой» совсем другую модель — игрушку из колец разной величины, которая имеет форму конуса. Эта ситуация может вызвать затруднения в запоминании и правильном применении геометрических терминов у детей. Данная проблема преодолевается при своевременном грамотном объяснении и разделении названий игрушек от названий их формы, эталонами для определения которой служат геометрические фигуры.
Задание 47
1. Нарисуйте пятиугольную пирамиду. Покажите ее основание, боковую поверхность, боковые грани и ребра. Какими геометрическими фигурами они являются?
2. Дайте определения высоты пирамиды и правильной пирамиды.
Тела вращения
Изучая форму окружающих предметов, дошкольники сталкиваются с телами вращения (рис. 78).
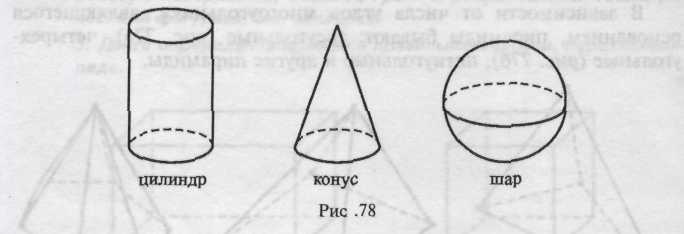
Эти фигуры называются телами вращения, так как они могут быть получены путем вращения некоторых плоских геометрических фигур.
Цилиндр – это тело вращения, которое может быть получено путем вращения прямоугольника вокруг одной из его сторон, как оси (рис. 79).
Конус — это тело вращения, которое может быть получено путем вращения прямоугольного треугольника вокруг одного из его катетов, как оси (рис. 80),
Шар — это тело вращения, которое может быть получено путем вращения половины круга вокруг его диаметра, как оси (рис. 81).
Определения этих фигур из курса геометрии средней школы:
Цилиндр – тело, которое состоит из двух кругов (оснований), совмещаемых параллельным
переносом, и всех отрезков, соединяющих

соответствующие точки этих кругов.
Конус – тело, которое состоит из круга (основания), точки (вершины), не лежащей в плоскости этого круга, и всех отрезков, соединяющих вершину конуса с точками основания.
Шар— тело, которое состоит из всех точек пространства, находящихся на расстоянии не более заданного (радиуса) от данной точки (центра).
Задание 48
— высоты цилиндре и прямого цилиндра;
— образующей конуса, высоты конуса и прямого конуса.
Дошкольники не знакомятся с этими формулировками, но могут различать и узнавать объемные тела, а если провести специальную работу, и правильно называть их. Дети усваивают свойства этих фигур в сравнении с другими. Например, во время игры «Катится — не катится» они выясняют, что: «Цилиндр, стоящий на основании, устойчив, как куб, но если его положить – катится, как шар».
Обследование поверхности дает знание того, что основанием цилиндра и конуса является круг. Рисование объемных предметов разной формы на плоскости учит детей сравнивать, проводить аналогию, моделировать, трансформировать пространство на плоскости. Например, в процессе обсуждения таких вопросов: «Какой формы мяч? Какую фигуру надо нарисовать, чтобы изобразить мяч?»
Знакомство с объемными фигурами расширяет знания детей об окружающем мире, закладывает основы для изучения геометрии в школе, обогащает их речь, формирует навыки обследования, развивает мышление.


Вопросы для самоконтроля к теме № 3
1. Что изучает геометрия?
2. Что изучает планиметрия?
3. Что изучает стереометрия?
4. Что называется геометрической фигурой?
5. Назовите правила построения геометрии.
6. Назовите основные фигуры на плоскости и в пространстве.
7. Какие фигуры называются плоскими?
8. Какие фигуры называются выпуклыми?
9. Дайте определение отрезка.
10. Дайте определение луча.
11. Дайте определение угла.
12. Какая линия называется ломаной?
13. Какая ломаная называется простой?
14. Дайте определение многоугольника.
15. Какой многоугольник называется выпуклым?
16. Какой многоугольник называется правильным?
17. Дайте определение треугольника.
18. Какой треугольник называется равносторонним, какой — равнобедренным, какой – разносторонним?
ТЕМА 4
ВЕЛИЧИНЫ И ИХ ИЗМЕРЕНИЕ
Понятие величины
Величина – одно из основных математических понятий, возникшее в древности и в процессе длительного развития подвергшееся ряду обобщений. Длина, площадь, объем, масса, скорость – это величины.
Задание 49
Приведите примеры различных величии, изучаемых в школе на уроках математики, физики, химии. Вспомните способы их измерения и единицы этих величин.
Величины представляют собой особые свойства реальных предметов или явлений, которые проявляются при сравнении их по этому свойству, причем каждая величина связана с определенным способом сравнения. Например, длину отрезков можно сравнить способом наложения, а массу предметов – взвешиванием. Величины можно оценивать количественно на основе сравнения.
Величину рассматривают как обобщение свойств некоторых объектов и как индивидуальную характеристику свойства конкретного объекта. Например, свойство предметов «иметь протяженность» называется «длиной».
Однородные величины – величины, которые выражают одно и то же свойство объектов некоторого класса. Например, длина, ширина, периметр — однородные величины.
Разнородные величины выражают различные свойства объектов (один предмет может иметь массу, объем и др.).
Источники:
http://mathhelpplanet.com/static.php?p=evklidovy-prostranstva
http://cyberpedia.su/14xfc19.html
http://lektsii.org/10-96516.html














