Сообщение на тему признаки делимости на 19. Основные признаки делимости

Сообщение на тему признаки делимости на 19. Основные признаки делимости

Признак делимости — это правило, позволяющее быстро определить, является ли число кратным заранее заданному числу, без необходимости выполнять деление. Рассмотрим несколько основных признаков деления:

Признак делимости на 2 n
Число делится на n-ю степень двойки тогда и только тогда, когда число, образованное его последними n цифрами, делится на ту же степень.

Признак делимости на 5 n
Число делится на n-ю степень пятёрки тогда и только тогда, когда число, образованное его последними n цифрами, делится на ту же степень.

Признак делимости на 10 n -1
Разобьем число на группы по n цифр справа налево (в самой левой группе может быть от 1 до n цифр) и найдем сумму этих групп, считая их n-значными числами. Эта сумма делится на 10 n – 1 тогда и только тогда, когда само число делится на 10 n – 1.

Признак делимости на 10 n
Число делится на n-ю степень десятки тогда и только тогда, когда n его последних цифр – нули.

Признак делимости на 10 n +1
Разобьем число на группы по n цифр справа налево (в самой левой группе может быть от 1 до n цифр) и найдем сумму этих групп с переменными знаками, считая их n-числами. Эта сумма делится на 10 n + 1 тогда и только тогда, когда само число делится на 10 n + 1.

Признак делимости на 2
Число делится на 2 тогда и только тогда, когда его последняя цифра делится на 2, то есть является чётной.

Признак делимости на 3
Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3.

Признак делимости на 4
Число делится на 4 тогда и только тогда, когда число из двух последних его цифр нули или делится на 4.

Признак делимости на 5
Число делится на 5 тогда и только тогда, когда последняя цифра делится на 5 (то есть равна 0 или 5).

Признак делимости на 6
Число делится на 6 тогда и только тогда, когда оно делится на 2 и на 3.

Признак делимости на 7
Число делится на 7 тогда и только тогда, когда результат вычитания удвоенной последней цифры из этого числа без последней цифры делится на 7 (например, 259 делится на 7, так как 25 — (2 · 9) = 7 делится на 7).

Признак делимости на 8
Число делится на 8 тогда и только тогда, когда три его последние цифры – нули или образуют число, которое делится на 8.

Признак делимости на 9
Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.

Признак делимости на 10
Число делится на 10 тогда и только тогда, когда оно оканчивается на ноль.

Признак делимости на 11
Число делится на 11 тогда и только тогда, когда сумма цифр с чередующимися знаками делится на 11 (то есть 182919 делится на 11, так как 1 – 8 + 2 – 9 + 1 – 9 = -22 делится на 11) — следствие факта, что все числа вида 10 n при делении на 11 дают в остатке (-1) n .

Признак делимости на 12
Число делится на 12 тогда и только тогда, когда оно делится на 3 и на 4.

Признак делимости на 13
Число делится на 13 тогда и только тогда, когда число его десятков, сложенное с учетверённым числом единиц, кратно 13 (например, 845 делится на 13, так как 84 + (4 · 5) = 104 делится на 13).

Признак делимости на 14
Число делится на 14 тогда и только тогда, когда оно делится на 2 и на 7.

Признак делимости на 15
Число делится на 15 тогда и только тогда, когда оно делится на 3 и на 5.

Признак делимости на 17
Число делится на 17 тогда и только тогда, когда число его десятков, сложенное с увеличенным в 12 раз числом единиц, кратно 17 (например, 29053→2905+36=2941→294+12=306→30+72=102→10+24=34. Поскольку 34 делится на 17, то и 29053 делится на 17). Признак не всегда удобен, но имеет определенное значение в математике. Есть способ немного попроще – Число делится на 17 тогда и только тогда, когда разность между числом его десятков и упятеренным числом единиц, кратно 17(например, 32952→3295-10=3285→328-25=303→30-15=15. поскольку 15 не делится на 17, то и 32952 не делится на 17)

Признак делимости на 19
Число делится на 19 тогда и только тогда, когда число его десятков, сложенное с удвоенным числом единиц, кратно 19 (например, 646 делится на 19, так как 64 + (6 · 2) = 76 делится на 19).

Признак делимости на 23
Число делится на 23 тогда и только тогда, когда число его сотен, сложенное с утроенным числом десятков, кратно 23 (например, 28842 делится на 23, так как 288 + (3 * 42) = 414 продолжаем 4 + (3 * 14) = 46 очевидно делится на 23).

Признак делимости на 25
Число делится на 25 тогда и только тогда, когда две его последние цифры делятся на 25 (то есть образуют 00, 25, 50 или 75)или число кратно 5.

Признак делимости на 99
Разобьем число на группы по 2 цифры справа налево (в самой левой группе может быть одна цифра) и найдем сумму этих групп, считая их двузначными числами. Эта сумма делится на 99 тогда и только тогда, когда само число делится на 99.

Признак делимости на 101
Разобьем число на группы по 2 цифры справа налево (в самой левой группе может быть одна цифра) и найдем сумму этих групп с переменными знаками, считая их двузначными числами. Эта сумма делится на 101 тогда и только тогда, когда само число делится на 101. Например, 590547 делится на 101, так как 59-05+47=101 делится на 101).

• Currently 3.98/5
• 1
• 2
• 3
• 4
• 5

Рейтинг: 4.0/5 (Всего оценок: 103)

Сайт учителя математики А.В.Капитановой

Признак делимости на 2

Число делится на 2 тогда и только тогда, когда его последняя цифра делится на 2, то есть является чётной.

Например:
2, 8, 16, 24, 66, 150 — делятся на 2, так как последняя цифра этих чисел четная;
3, 7, 19, 35, 77, 453 — не делятся на 2, так как последняя цифра этих чисел нечетная.

Признак делимости на 3

Число делится на 3 тогда и только тогда, когда сумма его цифр делится на 3.

Например:
471 — делится на 3, так как 4+7+1=12, и число 12 делится на 3;
532 — не делится на 3, так как 5+3+2=10, а число 10 не делится на 3.

Признак делимости на 4

Число делится на 4 тогда и только тогда, когда две его последние цифры составляют число, которое делится на 4. Двузначное число делится на 4 тогда и только тогда, когда удвоенное число десятков, сложенное с числом единиц делится на 4.

Например:
4576 — делится на 4, так как число 76 (7·2+6=20) делится на 4;
9634 — не делится на 4, так как число 34 (3·2+4=10) не делится на 4.

Признак делимости на 5

Число делится на 5 тогда, когда последняя цифра делится на 5, т.е. если она 0 или 5.

Например:
375, 5680, 233575 — делятся на 5, так как их последняя цифра равна 0 или 5;
9634, 452, 389753 — не делятся на 5, так как их последняя цифра не равна 0 или 5.

Признак делимости на 6

Число делится на 6 тогда и только тогда, когда оно делится и на 2, и на 3, то есть если оно четное и сумма его цифр делится на 3.

Например:
462, 3456, 24642 — делятся на 6, так как они делятся одновременно и на 2 и на 3;
861, 3458, 34681 — не делятся на 6, так как 861 не делится на 2, 3458 не делится на 3, 34681 не делится на 2.

Признак делимости на 7

Число делится на 7, если разность между числом десятков и удвоенной цифрой единиц делится на 7.

Число 296492
Берем последнюю цифру “2”, удваиваем, получаем 4. Вычитаем 29649-4=29645. Неизвестно, делится ли оно на 7. Поэтому проверим снова.
Берем последнюю цифру “5”, удваиваем, получаем 10. Вычитаем 2964-10=2954. Неизвестно, делится ли оно на 7. Поэтому проверим снова.
Берем последнюю цифру “4”, удваиваем, получаем 8. Вычитаем 295-8=287. Неизвестно, делится ли оно на 7. Поэтому проверим снова.
Берем последнюю цифру “7”, удваиваем, получаем 14. Вычитаем 28-14=14. Число 14 делится на 7, значит и исходное число делится на 7

Признак делимости на 8

Число делится на 8 тогда и только тогда, когда число, образованное тремя его последними цифрами, делится на 8. Трёхзначное число делится на 8 тогда и только тогда, когда число единиц, сложенное с удвоенным числом десятков и учетверённым числом сотен, делится на 8.

952 делится на 8 так как на 8 делится 9*4+5*2+2=48

Признак делимости на 9

Число делится на 9 тогда и только тогда, когда сумма его цифр делится на 9.

Например:
468, 4788, 69759 — делятся на 9, так как сумма их цифр делится на девять (4+6+8=18, 4+7+8+8=27, 6+9+7+5+9=36);
861, 3458, 34681 — не делятся на 9, так как сумма их цифр не делится на девять (8+6+1=15, 3+4+5+8=20, 3+4+6+8+1=22).

Признак делимости на 10

Число делится на 10 тогда и только тогда, когда оно оканчивается на нoль.

Например:
460, 24000, 1245464570 — делятся на 10, так как последняя цифра этих чисел равна нулю;
234, 25048, 1230000003 — не делятся на 10, так как последняя цифра этих чисел не равна нулю.

Признак делимости на 11

Признак 1: число делится на 11 тогда и только тогда, когда модуль разности между суммой цифр, занимающих нечётные позиции, и суммой цифр, занимающих чётные места делится на 11.

Например, 9163627 делится на 11, так как делится на 11.

Другой пример — 99077 делится на 11, так как делится на 11.

Признак 2: число делится на 11 тогда и только тогда, когда на 11 делится сумма чисел, образующих группы по две цифры (начиная с единиц).

Например, 103785 делится на 11, так как на 11 делятся и

Признак делимости на 13

Признак 1: Число делится на 13 тогда, когда сумма числа десятков с учетверенным числом единиц делится на 13.

Например 845 делится на 13, так как на 13 делятся и

Признак 2: Число делится на 13 тогда, когда разность числа десятков с девятикратным числом единиц делится на 13.

Например 845 делится на 13, так как на 13 делятся

Признак делимости на 17

Число делится на 17 тогда, когда модуль разности числа десятков и пятикратного числа единиц делится на 17.

Например, 221 делится на 17, так как делится на 17.

Число делится на 17 тогда, когда модуль суммы числа десятков и числа двенадцать умноженной на кол-во единиц делится на 17.

Например, 221 делится на 17, так как делится на 17.

Признак делимости на 19

Число делится на 19 тогда и только тогда, когда число десятков, сложенное с удвоенным числом единиц, делится на 19.

Например, 646 делится на 19, так как на 19 делятся и

Признак делимости на 20

Число делится на 20 тогда и только тогда, когда число, образованное двумя последними цифрами, делится на 20.

Другая формулировка: число делится на 20 тогда и только тогда, когда последняя цифра числа — 0, а предпоследняя — чётная.

Признаки делимости на 23

Признак 1: число делится на 23 тогда и только тогда, когда число сотен, сложенное с утроенным числом, образованным двумя последними цифрами, делится на 23.

Например, 28842 делится на 23, так как на 23 делятся и

Признак 2: число делится на 23 тогда и только тогда, когда число десятков, сложенное с семикратным числом единиц, делится на 23. Например, 391 делится на 23, так как делится на 23.

Признак 3: число делится на 23 тогда и только тогда, когда число сотен, сложенное с семикратным числом десятков и утроенным числом единиц, делится на 23.

Например, 391 делится на 23, так как делится на 23.

Признак делимости на 25

Число делится на 25 тогда и только тогда, когда две его последние цифры составляют число, которое делится на 25.

Признак делимости на 27

Число делится на 27 тогда и только тогда, когда на 27 делится сумма чисел, образующих группы по три цифры (начиная с единиц).

Признак делимости на 29

Число делится на 29 тогда и только тогда, когда число десятков, сложенное с утроенным числом единиц, делится на 29.

Например, 261 делится на 29, так как делится на 29.

Признак делимости на 30

Число делится на 30 тогда и только тогда, когда оно заканчивается на 0 и сумма всех цифр делится на 3.

Например: 510 делится на 30, а 678 – нет.

Признак делимости на 31

Число делится на 31 тогда и только тогда, когда модуль разности числа десятков и утроенного числа единиц делится на 31. Например, 217 делится на 31, так как делится на 31.

Признак делимости на 37

Признак 1: число делится на 37 тогда и только тогда, когда при разбивании числа на группы по три цифры (начиная с единиц) сумма этих групп кратна 37.

Признак 2: число делится на 37 тогда и только тогда, когда на 37 делится модуль утроенного числа сотен, сложенного с учетверённым числом десятков, за вычетом числа единиц, умноженного на семь.

Например, число 481 делится на 37, так как на 37 делится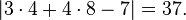

Признак 3: число делится на 37 тогда и только тогда, когда на 37 делится модуль суммы числа сотен с числом единиц, умноженного на десять, за вычетом числа десятков, умноженного на 11.

Например, число 481 делится на 37, так как на 37 делится

Признак делимости на 41

Признак 1: число делится на 41 тогда и только тогда, когда модуль разности числа десятков и четырёхкратного числа единиц делится на 41.

Например, 369 делится на 41, так как делится на 41.

Признак 2: чтобы проверить, делится ли число на 41, его следует справа налево разбить на грани по 5 цифр в каждой. Затем в каждой грани первую справа цифру умножить на 1, вторую цифру умножить на 10, третью — на 18, четвёртую — на 16, пятую — на 37 и все полученные произведения сложить. Если результат будет делиться на 41, тогда и только тогда само число будет делиться на 41.

Признак делимости на 50

Число делится на 50 тогда и только тогда, когда число, образованное двумя его младшими десятичными цифрами, делится на 50.

Признак делимости на 59

Число делится на 59 тогда и только тогда, когда число десятков, сложенное с числом единиц, умноженное на 6, делится на 59. Например, 767 делится на 59, так как на 59 делятся и

Признак делимости на 79

Число делится на 79 тогда и только тогда, когда число десятков, сложенное с числом единиц, умноженное на 8, делится на 79. Например, 711 делится на 79, так как на 79 делятся .

Признак делимости на 99

Число делится на 99 тогда и только тогда, когда на 99 делится сумма чисел, образующих группы по две цифры (начиная с единиц). Например, 12573 делится на 99, так как на 99 делится

Признак делимости на 101

Число делится на 101 тогда и только тогда, когда модуль алгебраической суммы чисел, образующих нечётные группы по две цифры (начиная с единиц), взятых со знаком «+», и чётных со знаком «-» делится на 101.

Например, 590547 делится на 101, так как на 101 делится

Доклад “Признаки делимости на 2, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 19, 25, 50”

Добавляйте авторские материалы и получите призы от Инфоурок

Еженедельный призовой фонд 100 000 Р

Частное общеобразовательное учреждение общая общеобразовательная школа «Полис-лицей»

Доклад на тему:

«Признаки делимости»

Учитель: Агеева Наталья Сергеевна Класс: 6

Город Дубна, 2018 г.

Если вы хотите научиться плавать, то смело входите в воду, а если хотите научиться решать задачи, то решайте их.

При изучении на уроках математики темы «Признаки делимости чисел на 2, 3, 5, 9,10» возник естественный вопрос: существуют ли признаки делимости, например, на 4, на 6, на 7, на 8, на 11 и т. д.? Если можно определить делимость чисел на эти числа, то должны быть признаки, по которым можно определить делимость натуральных чисел на другие числа. Такие признаки существуют. Признаки делимости чисел – это правила, позволяющие не производя деления сравнительно быстро выяснить, делится ли это число на заданное без остатка. Признаки делимости изучали ученые разных времен и народов.

Из истории математики о делимости чисел

Огромный вклад в изучение признаков делимости натуральных чисел внес Б. Паскаль.
БЛЕЗ ПАСКАЛЬ (Blaise Pascal) (1623–1662), французский религиозный мыслитель, математик и физик, один из величайших умов 17 столетия. Родился в Клермон-Ферране (провинция Овернь) 19 июня 1623. Юный Блез очень рано проявил выдающиеся математические способности, научившись считать раньше, чем читать Свой первый математический трактат «Опыт теории конических сечений» он написал в 24 года. Примерно в это же время он сконструировал механическую суммирующую машину, прообраз арифмометра. Работы Паскаля в области точных наук, или ранний период его творчества относится к 1640-1650 году. За эти 10 лет разносторонний ученый сделал очень много: он нашел алгоритм для нахождения признаков делимости любого целого числа на любое другое целое число, сформулировал способ вычисления биноминальных коэффициентов, изложил ряд основных положений элементарной теории вероятности, впервые точно определил и применил для доказательства метод математической индукции. Вместе с Галилеем и Стевином Паскаль разработал основные положения классической гидростатики и установил ее основной закон – «Закон Паскаля». Умер Паскаль в Париже в 1662 году.

Признак делимости Паскаля.

Натуральное число а разделится на другое натуральное число b только в том случае, если сумма произведений цифр числа а на соответствующие остатки, получаемые при делении разрядных единиц на число b, делится на это число.

Например,: число 2814 делится на 7, так как делится на 7. (Здесь 6-остаток отделения 1000 на 7, 2- остаток от деления 100 на 7 и 3- остаток от деления 10 на 7).

Делители и кратные .

Если натуральное число а делится нацело на натуральное число b , то число а называют кратным числам b , а число b – делителем числа а .

Для любого натурального числа а каждое из чисел а*1, а*2, а*3, а*4, … является кратным числа а .

Простые и составные числа.

Натуральное число называют простым , если оно имеет только два натуральных делителя: единицу и само это число.

Например, число 5 – простое, т.к. делится на 1 и само на себя.

Натуральное число называют составным , если оно имеет больше двух натуральных делителей.

Например, число 55 – составное, т.к. имеет более двух делителей: 1; 5; 11; 55.

Число 1 не относится ни к простым, ни к составным числам.

Делимость чисел обладает свойствами :

Если каждое из слагаемых делится на какое-то число, то и сумма их обязательно делится на это же число.

Если каждое слагаемое, кроме одного, делится на какое-нибудь число, а одно не делится, то сумма не делится на это число.

Если уменьшаемое и вычитаемое делится на какое-нибудь число, то и разность разделится на это число.

Если только одно из чисел – уменьшаемое или вычитаемое – делится на какое-нибудь число, а другое не делится, то и разность не делится на это число.

Если хоть один из множителей делится на какое-нибудь число, то произведение их также разделится на это число.

Признаки делимости на 2

Чётное число – это число, которое делится на 2.

Нечётное число – не делится на 2.

Число делится на два, в том случае если его последняя цифра является чётной или нуль. Во всех остальных случаях – не делится.

Число 55 734 делится на 2, так как у него последняя цифра 4 которая является чётной.

Число 559 не делится на 2, так как цифра 9 находящаяся в конце нечетная.

Число 6750 делится на 2, так как цифра, которая находится в конце 0.

Признаки делимости на 3

Если сумма цифр числа делится нацело на 3, то и само число делится нацело на 3. Если сумма цифр числа не делится нацело на 3, то и само число не делится нацело на 3.

2721 = 2+7+2+1 = 12, 12 делится на 3, значит, и само число делится на 3.

Признаки делимости на 4

Число делится на 4, при условии, если две последние его цифры нули либо образуют число, которое делится на 4. В остальных случаях – не делится.

Число 52 600 делится на 4, так как в его окончании находятся два нуля.

Число 768 001 не делится на 4, так как крайние две цифры дают число 01, которое не делится на 4.

Число 67 144 делится на 4, так как две конечные цифры 4 и 4 дают число 8, которое делится на 4.

Признаки делимости на 5

Если запись натурального числа оканчивается цифрой 0 или 5, то это число делится нацело на 5. Если запись натурального числа оканчивается любой цифрой, отличной от 0 или 5, то это число не делится нацело на 5.

245 делится на 5, так как число оканчивается цифрой 5.

6740 делится на 5, так как число оканчивается цифрой 0.

657 не делится на 5, так число оканчивается цифрой 7.

Признаки делимости на 6

Число делится на 6, когда его можно разделить одновременно на 2 и на 3. В противном случае – не делится.

Число 306 может быть разделено на 6, в виду того, что оно делится и на 2 и на 3.

Признаки делимости на 7

Число делится на 7, если результат вычитания удвоенной последней цифры из числа десятков этого числа делится на 7 или равен 0.

959 делится на 7, потому что 95-2*9=95-18=77, 77_7=11 (77 делится на 7 без остатка).

111 и 345 не делятся на 7, потому что 11-2*1=11-2=9 (9 не делится без остатка на 7) и 34-2*5=34-10=24 (24 не делится без остатка на 7).

Признаки делимости на 8

Число делится на 8 только тогда, когда число из трех последних цифр делится на 8.

56064 – 064 делится на 8, значит, 56064 кратно 8.

Признаки делимости на 9

Если сумма цифр числа делится нацело на 9 то и само число делится нацело на 9. Если сумма цифр числа не делится нацело на 9, то и само число не делится нацело на 9.

6003 = 6+0+0+3 = 9, 9 делится на 9, значит, и само число делится на 9.

Признаки делимости на 10

Если запись натурального числа оканчивается цифрой 0, то это число делится нацело на 10. Если запись натурального числа оканчивается любой цифрой, отличной от 0, то это число не делится нацело на 10.

991186 0 – делится на 10.

Признаки делимости на 11

На 11 можно разделить только те числа, у которых сумма цифр, находящихся на нечётных местах, или равна сумме цифр, находящихся на чётных местах, либо отличны от нее на число, которое делится на 11.

103 785 можно разделить на 11, так как 1 + 3 + 8 = 12 и 0 + 7 + 5 = 12

461 025 не может разделено на 11, в виду того что числа 7 и 11 взаимно не равны, а их разность 4 на 11 не разделить. ( 11 – 7 = 4 ),( 4 + 1 + 2 = 7 ), ( 6 + 0 + 5 = 11).

Признаки делимости на 12

Число делится на 12 в том, и только в том случае если оно одновременно делится на 3 и 4.

504 – делится на 3 и 4, а значит и на 12.

Признаки делимости на 13

Число делится на 13 когда результат вычитания последней цифры умноженной на 9 из этого числа без последней цифры делится на 13.

858 делится на 13, так как 85-9*8 = 13 делится на 13.

Признаки делимости на 14

Число делится на 14 когда оно делится на 2 и на 7.

Число 252 делится на 2 и на 7, значит, оно делится и на 14.

Признаки делимости на 15

Число делится на 15, если оно делится на 5 и на 3, т.е. чтобы оно оканчивалось 0 или 5 и, кроме того, сумма его цифр делилась на 3.

370 5 – 3+7+0+5 = 15, значит, число кратно 3.

Признаки делимости на 19

Число делится на 19 когда число его десятков, сложенное с удвоенным числом единиц, делится на 19. Например; требуется определить, делится ли на 19 число 1026.

Числа кратные 19 всегда делятся на 19.

19, 38, 57, 76, 95, 114, 133, 152, 171, 190, 209, 228..

Применим последовательно признак делимости. Число десятков в признаке надо считать не цифру в разряде десятков, а общее число целых десятков во всем числе.

В результате выполнения последовательных двух шагов мы получили число 19, которое делится на 19, следовательно, число 1026 делится на 19.

Признаки делимости на 25

Число делится на 25 когда две его последние цифры либо нули, либо образуют число, делящееся на 25.

58050 делится на 25, так как 50 делится на 25.

579 00 делится на 25.

Признаки делимости на 50

Чтобы число делилось на 50, надо, чтобы на конце числа две последние цифры делились на 25 и представляли четное число. Этому условию удовлетворяют числа 50 и 100, но 100 – трехзначное число, значит, запись числа должна оканчиваться на 00 или 50.

Кроме известных признаков делимости на 2, 3, 5, 9 и 10 существуют признаки делимости на 4, 6, 7, 8, 11, 12, 13, 14, 15, 19 и 25. В некоторых случаях без признаков делимости просто невозможно обойтись.

Применение признаков делимости чисел в изучении математики является эффективным. Знание их значительно ускоряет решение многих заданий. Предложенный материал «Признаки делимости чисел» можно использовать как на уроках математики, так и во внеклассных занятиях учащимися 5-9-х классов. Учителям – с целью подготовки учащихся к решению ОГЭ, ГИА, ЕГЭ, олимпиадных задач, интеллектуальным конкурсам, региональному конкурсу «Кенгуру».

1. И. Я. Депман «История арифметики» Москва 1965 Издательство «Просвещение»

2. Г. И. Глейзер «История математики в школе 7 – 8 классы» Москва 1982 «Просвещение»

3. «1001 вопрос и ответ. Большая книга знаний» Москва 2004 «Мир книги»

4. «Математика» Москва 1999 «Первое сентября»

5. «Математика» Москва 2000 «Первое сентября»

6. «Математика» Москва 2002 «Первое сентября»

7. «Избранные вопросы математики. 9 кл. Факультативный курс». – М.: Просвещение, 1979.

8. «Избранные задачи и теоремы элементарной математики. Арифметика и алгебра»/ Д. О. Шклярский, Н. Н. Ченцов, И. М. Яглом – 5-е изд. – М.: Издательство «Наука», 1977.

9. «Дополнительные главы по курсу математики. Учебное пособие по факультативному курсу для учащихся 7-8 классов»/ К. П. Сикорский – издание 2-е, исправленное и дополнительное – М.: «Просвещение», 1974.

10 . Энциклопедический словарь юного математика / Сост.А.П.Савин.-М.: Педагогика, 1989.- 352 с.

11. Я.И. Перельман. Занимательная Алгебра, – М.: Триада-Литера, 1994.-199с.

· Воробьев КН., Признаки делимости, издательство
«Наука», 1974.

12. Кордемский Б. А., Математическая смекалка, Ленинград,
издательство технико-теоретической литературы, 1956.

13. Перельман Я.И., Занимательная алгебра, Москва,
издательство «Наука», 1988.

14 .И. Я. Депман, Н.Я. Виленкин « За страницами учебника математики» М. Просвещение. 1989 г. стр.97.

15. М. Б. Гельфанд, В.С. Павлович «Внеклассная работа по математике в 8-летней школе» М. Просвещение. 1965 г. стр.37.

16. Журнал «Математика в школе» №5 за 1999 г. стр.40.

17. Математика – это интересно! – М.: ТЕРРА – Книжный клуб, 2006 год. Пельман Я. И.

18. Внеклассная работа по математике 5-11 классы М.: Айрис – пресс 2007 год Фарков А. В.

19. Оригинальные головоломки с числами. М.: Эксмо, 2007. Кен Рассел, Филипп Картер.

20. Внеклассная работа по математике в 6-8 классах. Москва. «Просвещение» 1984 г. В. А. Гусев, А. И. Орлов, А. Л. Розенталь.

Источники:

http://www.math.com.ua/articles/priznaki-delimosti-chisel.html
http://ychitelll.ucoz.ru/index/priznaki_delimosti/0-73
http://infourok.ru/doklad-priznaki-delimosti-na-3512214.html