Как называется цифра 1. В чем разница между числом и цифрой? Другие системы счисления

Лекция 6. Системы счисления

Как только люди стали общаться, т.е. передавать информацию, они стали считать. Первыми инструментами счета были пальцы рук и простые предметы. Затем расчеты стали фиксировать, что привело к появлению систем счисления.

Система счисления– это свод приемов обозначения и записи чисел при помощи специальных символов – цифр.

Система счисления — это система отображения любого числа с по­мощью ограниченного количества условных знаков, называемых циф­рами.

Сначала люди придумали непозиционные или кодовые системы счисления (IV тысячелетие до н.э.), в которых расположение цифр в числе не имеет значения и для обозначения каждого числа существует свой символ.

Но в непозиционных системах трудно записывать большие числа и выполнять арифметические действия. Более совершенной системой (переходной от непозиционных систем к позиционным) стала – римская (500 лет до н.э.), которая применяется и в наше время. Алфавитом (цифрами) этой системы служат символы:

I (1)

V (5)

X (10)

L (50)

C (100)

D (500)

M (1000)

Здесь уже положение цифры в числе меняет ее значение. Например, в числеIV I отнимается от V, а в числе VI – прибавляется к V. Число 1995 в этой системе запишется так: MCMXCV.

Но и этой системе присущи все недостатки непозиционных систем. Чтобы от них избавиться понадобились позиционные системы.

Если место, занимаемое символом в записи числа, придает этому символу определенное значение, то такая система счисления называется позиционной.

Количество цифр системы (символов алфавита) называется ее основанием, место цифры в числе – разрядом, а количество цифр в числе – его разрядностью.

Индо-арабская десятичная система (VI в.) наиболее естественна для человека, т.к. считать мы учимся на пальцах, а их на двух руках как раз 10. В этой системе 10 цифр: от 0 до 9. Каждая цифра в числе при перемещении справа налево в следующий разряд увеличивает свое значение в 10 раз.
Любое число может быть представлено в виде суммы, где каждое слагаемое представляет собой произведение коэффициента (цифры числа) на основание системы (10) в степени, равной разряду этой цифры.

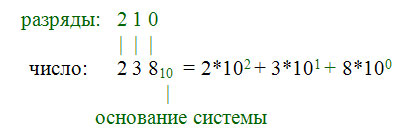
Итак, основание системы счисления – это количество цифр (символов алфавита) в ней. Какое число можно принять за основание системы? Любое натуральное, например, 1. В этом случае мы получаем унарную систему счисления, древнейшую в истории культуры счета. В ней для записи чисел применяется только один символ (камешек, палочка, зарубка). Число в ней – это количество таких символов.

Какая разница между числом и количеством? Одно и то же количество может быть выражено разными числами. Числа записываются с помощью цифр. Не следует путать понятия: цифра, число, количество. Использовать текстовую информацию позволяет алфавит, а количественную — системы счисления.

Давайте докажем, что цифра — это условный знак для записи чисел. Возьмем число 8 136 547. Теперь представим себе, что цифра 3 обо­значается как Δ , цифра 4 как , цифра 5 как ○, остальные же цифры остались прежними. При таких обозначениях цифр наше число будет выглядеть так:

Как вы думаете, изменилось ли количество, которое определяется этим числом? Конечно, нет. Изменился вид самого числа, да и то по­тому, что изменились условные знаки, называемые цифрами.

Трудно определить, сколько всего существует систем счисления. Скорее всего, бесконечное множество. В позиционных системах счислениявес цифры зависит от места (позиции), которую она занимает в числе.

Мы помним, что в записи числа используются позиции (разряды) единиц, десятков, сотен, тысяч, десятков тысяч, т. е. число можно пред­ставить в следующем виде:

35 876 = 6*1 + 7*10 + 8*100 + 5*1000 + 3*10 000 .

Цифра 5, входящая в число 35 876, обозначает пять тысяч, потому что она находится именно в той позиции, в которой указывается ко­личество тысяч, или, иными словами, именно нахождение в данной позиции определяет ее вес. В числе 68952 тоже есть цифра 5, но ее вес, определяемый позицией в этом числе, составляет пять десятков.

В непозиционных системах счислениятакой закономерности нет, т.е. вес цифры не зависит от ее позиции в числе. Классический при­мер непозиционной системы счисления — римская система, которая используется до сих пор, правда в основном для нумерации.

Особый интерес из позиционных систем для нас представляют такие, веса которых являются членами геометрической прогрессии. Рассмотрим несколько рядов чисел:

1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1 024, 2 048 .

1, 3, 9, 27, 81, 243, 729, 2 187, 6561, 19683, 59045 .

1, 4, 16, 256, 1024, 4096, 16384, 65536, 262 144 .

1, 5, 25, 125, 625, 3125, 15 625, 78 125, 390 625 .

Что общего в этих рядах чисел? Каждое следующее число в них получается из предыдущего путем умножения его на конкретное число. В первом ряду это 2, во втором 3, в третьем 4, в четвертом 5 и т.д.

Такой ряд чисел называется геометрической прогрессией, сами чис­ла ряда — это члены геометрической прогрессии, а то число, умножая на которое предыдущий (или n-й) член прогрессии, мы получаем по­следующий, или (п + 1)-й, является знаменателем геометрической прогрессии, обозначим его р.

Давайте теперь представим десятичное число 64572 187 в весовом виде:

64 572 187 = 7*1 + 8*10 + 1*100 + 2*1000 + 7*10000 + 5*100000 + 4* 1000000 + 6*10000000

и в виде таблицы по весам позиций и цифрам в этих позициях:

Вес позиции. 1 10 100 1000 10000 100000 1000000 100000000

Цифра. 7 8 12 7 5 4 6

Видно, что веса привычной нам десятичной системы счисления являются членами геометрической прогрессии, знаменателем такой прогрессии выступает число 10, т.е. р = 10, оно называется основани­ем системы счисления, а сама система называется р-ричной системой счисления.

Запишем теперь число из таблицы с использованием сте­пеней числа 10 — основания десятичной системы счисления:

64572 187 = 7*10 0 + 8*10 1 + 1*10 2 + 2*10 3 + 7*10 4 + 5*10 5 + 4*10 6 + 6*10 7 . (1)

Теперь попробуем записать представления числа по степеням осно­вания р-ричной системы счисления в общем виде:

(2)

где a_i — цифра, находящаяся в позиции, имеющей вес i = п, п – 1, п – 2, . 2, 1, 0 соответственно; п, п – 1, п – 2, . 2, 1, 0 — веса позиций, или степень, в которую возводится р в данной позиции; р — основание системы счисления.

Но ведь число может иметь и дробную часть, а веса позиций в дроб­ной части — числа отрицательные. Рассмотрим пример десятичного дробного числа 0,874562. Веса позиций, если идти от десятичной за­пятой вправо, таковы:

Если использовать десятичные дроби, то веса будут выглядеть следующим образом:

0,1; 0,01; 0,001; 0,0001; 0,00001; 0,000001,

или то же самое с использованием отрицательных степеней числа 10:

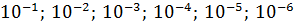
Значит, аналогично записи (1) предложенное дробное число мож­но представить так:

Следовательно, выражение (2) для чисел, имеющих как целую, так и дробную часть, примет следующий вид:

(3)

Мы говорили о том, что любая система счисления использует огра­ниченное число условных знаков — цифр. Оказывается, что количество этих знаков равно основанию системы р. И действительно, в десятич­ной системе их десять, это 0, 1,2, 3, 4, 5, 6, 7, 8, 9. А сколько их долж­но быть, например, в шестеричной системе счисления, т. е. когда р = 6. Цифр будет шесть, это 0, 1, 2, 3, 4, 5. А в восьмеричной? Восемь, это 0, 1, 2, 3, 4, 5, 6, 7.

Сформулируем правило: количество цифр в р-ричной системе счис­ления равно р, причем это цифры от 0 до (р – 1).

Как быть, если основание системы больше 10, например 12 или 16?

В этом случае на помощь приходят буквы латинского алфавита: А, В, С, D и т.д. Правда в этом случае они называются уже не буквами, а цифрами. Итак, основание системы счисления может быть любым, все системы равноправны, но тем не менее мы используем десятичную систему счисления. Причина проста: на руках 10 пальцев — это, на­верное, и есть наш первый «вычислитель».

Особо мы будем еще рассматривать двоичную систему счисления, поскольку она более удобна для использования в компьютерах. Основным элементом, который хранит 1 бит информации в ком­пьютере, является триггер. Для хранения нескольких бит информации используются столько элементов, сколько бит надо хранить. Как пра­вило, эти элементы и есть триггеры, в этом случае они образуют ин­тегральную схему, которая называется регистром.

Если попытаться дать более строгое определение, то регистр — это совокупность эле­ментов, которые могут принимать, хранить и выдавать информацию в компьютере. Регистры играют очень большую роль в работе микропроцессора компьютера и других его частей.

Задание: ответить на вопросы учебника Цв. Стр.54, вопр. 1-5.

185.94.188.243 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Как называется цифра 1. В чем разница между числом и цифрой? Другие системы счисления

Готов узнать, чем отличаются цифры от чисел? Не будем тянуть единицу за чуб, а двойку за хвост, рассказываем!

Что такое цифра?

Чтобы разобраться в отличиях между числами и цифрами, для начала запомни несколько простых утверждений:

Цифры – это единицы счета от 0 до 9, остальные все – числа.

Числа состоят из цифр.

Цифры являются знаками, а каждое число – это количественная абстракция.

Слово «цифра» происходит от арабского «сифр» , что означает «ноль». Цифры – это знаки для записи чисел. Обычно цифра означает один из следующих графических знаков: 0 1 2 3 4 5 6 7 8 9. Это так называемые арабские цифры.

Однако кроме арабской существует много других систем счисления, и они настолько отличаются, что число одной из них может оказаться цифрой в другой.

Римские цифры, например, записывают так: I V X L C D M. Поэтому арабское число «10» в римской системе счисления будет цифрой «Х» (десять), которая обозначается латинской буквой.

Шестнадцатеричные цифры, которые чаще всего используют разработчики компьютеров и программисты, на письме обозначают следующим образом: 0 1 2 3 4 5 6 7 8 9 A B C D E F. В этой системе счисления арабские цифры от 0 до 9 соответствуют значениям от нуля до девяти, а шесть латинских букв A, B, C, D, E, F соответствуют значениям от десяти до пятнадцати.

Каждое число шестнадцатеричной системы счета записывается с помощью 16-ти цифр.

В некоторых языках (древнегреческом, церковнославянском, иврите) существует система записи чисел буквами.

Как написать цифры на иврите.

Что называют числом?

Число – это один из основных объектов , который используют для подсчета, измерения и маркировки.

Символы, применяемые для обозначения чисел, называются цифрами .

Кроме использования цифр при счете и измерении, ими пользуются для маркировки (к примеру, телефонный номер) и упорядочения (например, универсальный идентификационный номер ISBN).

Подытоживая выше сказанное, делаем вывод, что число может указывать на символ, слово или математическую абстракцию.

Но интересно, что кроме практического применения, числа имеют также культурное значение. На Западе, например, число 13 считают несчастливым, а «миллион» часто может означать просто «много».

Казалось бы, все знают, что такое цифра и число. Но если поставить вопрос по-другому: “А число от цифры?” , то многие затруднятся с ответом. Для того, чтобы приступить к отличиям, следует дать точное определение этим понятиям.

Что такое цифра?

Цифра – это упорядоченная знаковая система, предназначенная для записи чисел. Цифрами считаются только те символы, которые в отдельности обозначают числа. Например, знак “-” хоть и применяется для того, чтобы записать число, но цифрой он не считается. Цифрами считается ряд от 0 до 9. Само слово “цифра” имеет арабские корни и обозначает “ноль” или “пустое место”. Эти символы бывают следующих видов:

Это перечислены самые известные разновидности. В разных языках, например, в древнегреческом, для записи чисел используют буквы. Чаще всего в обиходной речи люди под словом “цифры” подразумевают числа, которыми записываются числовые данные. Следует помнить, что отрицательных, дробных и натуральных цифр не существует.

Привычная нам система исчисления основывается на цифрах арабского происхождения, которые стали известны европейцам в 13-м веке. До этого для записи чисел использовали римские графические символы. Сейчас эту разновидность можно увидеть на циферблате часов, а также в книгах.

Число – это основное математическое понятие. Его используют для:

• количественной характеристики;
• сравнения;
• обозначения нумерации объектов.

Числа записываются цифрами и иногда при помощи символов операций в математике. Они возникли еще в первобытном обществе, когда появилась потребность в счете. Числа бывают:

• натуральные – получаются при естественном счете;
• целые – получаются при помощи объединения натуральных чисел;
• рациональные – имеют вид дроби;
• действительные;
• комплексные.

Два последних вида чисел имеют важное значение для математического анализа и получаются благодаря расширению рациональных (для действительных) и действительных (для комплексных) чисел.

Если в древние времена числа были нужны для перечисления, то с научным прогрессом их значение возросло.

1. С числами можно проводить различные математические действия. С цифрами такого делать нельзя.
2. Число может быть отрицательным, дробным, в отличие от цифр.
3. Количество цифр всего 10, а чисел – бесконечное множество, т.к. они состоят из цифр.

Кроме различий, с математической точки зрения, существуют и лингвистические отличия. Они рассматривают, в каких случаях можно говорить “цифра”, а когда – “число”. Если в разговоре упоминаются официальные показатели, то уместно говорить слово “цифра”. Это могут быть, например, статистические данные.

Понятие “цифры” широко распространено в нумерологии. Нумерологи используют это понятие как знак, который способен влиять на судьбу человека. Они наделяют его мистическими свойствами. Например, нумерологи уверены в том, что некоторые цифры притягивают удачу.

Число употребляют тогда, когда нужно назвать количество чего-либо, или когда речь идет о календарной дате или дне месяца. В русском языке для употребления этого понятия применяются порядковые числительные.

По сравнению с первобытными и древними обществами, у понятия “цифра” расширилась область употребления. Теперь это – не только в математике. Сейчас люди говорят о цифровом телевидении, цифровом формате. Так же и с числами – теперь они применяются, например, в информатике. Получается, что с развитием общества и науки развиваются и математические понятия. После прочтения всех математических и лингвистических тонкостей читатели знают, чем отличается число от цифры.

Термин “число” возникло в древние времена, когда у людей впервые получилось посчитать предметы. Первое время счёт вёлся на пальцах. Затем начали считать по зарубками на палочках. Со временем люди стали понимать числа свободно от предметов и лиц, которые могли подвергаться счёту. Поэтому у славян возникло слово “число”.

В XV веке в европейских странах начали распространяться специальные знаки, с помощью которых обозначались числа (числа: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0). Это было изобретением индейцев, а позже они появились в Европе благодаря арабам (арабские цифры). Почему они именно такие, какие есть?

Если посмотреть внимательно на эти арабские числа, то можно заметить, что каждое число соответствует количеству углов, которое можно найти на этой цифре. У числа 0 нет углов, у числа 1 – один угол, а у 9 – все девять углов.

С середины ХVIII века у слова цифра появилось новое значение — знак числа.

В чем разница между цифрой и числом?

Итак, у слова число и цифра различное значение и происхождение. Число — единица счёта, которая выражает количество (один дом, два дома, и т.д.). Цифра — знак (символ), который обозначает значение числа. Для записи чисел используются арабские цифры — 1, 2, 3… 9, иногда и римские — I, II, III, IV, V и т.д.

В разговоре слова число и цифра заменяют друг друга. Например, под числом мы понимаем не только величину, но и знак, выражающий её.

Названия и последовательность натуральных чисел от 1 до 20

Числа 1,2,3,4,5,6,7,8,9,0, которые используются при счёте- это натуральные числа. С помощью цифр 0,1,2,3,4,5,6,7,8,9 можно записать натуральное число. Такая запись чисел называется десятичной. В каждом классе присутствует три разряда.

• Приведём ниже таблицу разрядов.

Классы Миллиарды Миллионы Тысячи Единицы

Разряд Сотни Десятки Единицы Сотни Десятки Единицы Сотни Десятки Единицы Сотни Десятки Единицы

1-е число 2 0 0 3 2 4 0 6 0 0 8 1

2-е число 4 7 0 0 0 0 2 0 2 3 0 0

3-е число 5 0 0 1 0 0 0 3 1 0 9 0

Вот так читаются некоторые числа:

• 1) десять миллиардов тридцать два миллиона четыреста шестьдесят девять тысяч восемь;
• 2) четыреста семьдесят миллиардов сто тридцать тысяч триста;
• 3) пять миллиардов три миллиона триста десять.

Существуют и такие классы: класс триллионов, класс квадриллионов, класс квинтиллионов.

Сравнение натуральных чисел

Сравнить два натуральных числа- значит установить, какое из них больше (меньше) другого. Результат сравнения записывается в виде неравенства с помощью знаков > (больше) и

Чем отличается цифра от числа

Все знают, что есть цифры и числа. Но если спросить: «Чем отличается цифра от числа?«, то многие дети, а порой и взрослые, затрудняются с ответом. А как объяснить эту разницу ребенку простыми словами?

Чтобы ответить на этот вопрос и понять в чём различие между цифрой и числом надо разобраться с понятиями, что такое цифра и что такое число.

Числа и цифры: в чем разница

Содержание

Что такое цифра?

Цифра — это письменный знак, изображающий число.

Что значит слово цифра? Это слово арабского происхождения и означает ноль или пустое место. Их существует только десять. Они придуманы для обозначения числа. Цифр всего 10.

0, 1, 2, 3, 4, 5, 6, 7, 8, 9

Что такое число?

Число — это основное математическое понятие.

Его используют для:

• количественной характеристики;
• сравнения;
• обозначения нумерации объектов.

Числа записываются при помощи цифр. Различают несколько видов чисел.

В древнейшие времена цифры обозначали прямолинейными пометками. Палочки до сих пор используются для обозначения римских цифр. Римских цифр 7.

I, V, X, L, C, D, M

Римские числа также, как и арабские, образуются при помощи цифр, только в данном случае римских.

В римских числах желательно разбираться, т.к. они часто используются не только в школьном курсе математики, но и в жизни. Например, на циферблате часов.

Отличия числа от цифры

1. С числами можно проводить различные математические действия. С цифрами такого делать нельзя.
2. Число может быть отрицательным, дробным, в отличие от цифр.
3. Количество арабских цифр всего 10 (римских — 7), а чисел — бесконечное множество, т.к. они состоят из цифр.

Надеюсь, что теперь вам всё понятно, и вы сможете без труда объяснить даже ребёнку, чем отличается число от цифры.

На уроках математики в начальной школе используется очень полезное упражнение. Детей просят дать характеристику числу. Другими словами рассказать о числе все, что знаешь. Не всем детям это задание даётся легко. Чтобы его выполнить пригодятся вышеописанные знания и не только.

Какие виды чисел изучаются в начальной школе?

В начальной школе рассматриваются: натуральные числа, число 0, доли и дроби.

Натуральные числа — используются для счёта предметов;

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11…

Однозначные числа — состоят из одной цифры;

1, 2, 3, 4, 5, 6, 7, 8, 9

Двузначные числа — состоят из двух цифр;

10, 11, 12, 13, 14, 15, 16, 17, 18, 19, 20 … 99

Соответственно самое маленькое двузначное число 10, а самое большое — 99.

Аналогично числа можно охарактеризовать как трёхзначные, четырёхзначные и т.д.

Иногда дети затрудняются назвать самое маленькое, например, пятизначное число (10 000) или самое большое семизначное (9 999 999). Просто полезно будет потренироваться это делать.

Чётные — числа, которые делятся пополам без остатка или же заканчиваются на 0, 2, 4, 6, 8;

2, 4, 6, 8, 10, 12, 14…

Нечетные — числа, которые не делятся на 2 без остатка;

1, 3, 5, 7, 9, 11, 13…

Круглые — числа, которые заканчиваются нулём.

10, 20, 30, 40, 50…

Как дать характеристику числу?

Разберём несколько примеров.

Число 7 — однозначное, нечетное, соседи числа 7 числа 6 и 8.

Также чисел первого десятка можно добавить такое дополнительное задание, как состав числа. Т.е. число 7 можно получить сложением чисел 1 и 6, 2 и 5, 3 и 4.

Число 10 — двузначное, чётное, круглое, соседи числа 9 и 11. Число 10 можно получить сложением чисел 1 и 9, 2 и 8, 3 и 7, 4 и 6, 5 и 5.

Чем крупнее число, тем больше можно о нём рассказать.

Число 999 — наибольшее трёхзначное число, нечётное, соседи 998 и 1000, в числе 9 сотен, 9 десятков и 9 единиц.

Надеюсь, что полученные знания были вам полезны и теперь вы знаете чем отличается цифра от числа, сможете объяснить это ребёнку простыми словами, а также потренироваться давать характеристику числам.

С уважением, Ольга Наумова

Благодарю, что поделились статьей в социальных сетях!

Источники:

http://studopedia.ru/9_200608_lektsiya–sistemi-schisleniya.html
http://artpos.ru/lunar-calendar/kak-nazyvaetsya-cifra-1-v-chem-raznica-mezhdu-chislom-i-cifroi.html
http://naymenok.ru/chem-otlichaetsya-tsifra-ot-chisla/